题目内容
8.曲线y=$\frac{1}{x}$(x>0)在点P(a,b)处的切线为L,若直线L与x,y轴的交点分别为A,B,则△OAB的周长的最小值为4$+2\sqrt{2}$.分析 利用导数求出函数y=$\frac{1}{x}$(x>0)在点 P(a,b)处的切线方程,得到直线在两坐标轴上的截距,由勾股定理求得第三边,作和后利用基本不等式求最值.
解答 解:由y=$\frac{1}{x}$,得y′=-$\frac{1}{{x}^{2}}$,
则$y′{|}_{x=a}=-\frac{1}{{a}^{2}}$,
∴y=$\frac{1}{x}$(x>0)在点P(a,b)处的切线方程为:y-$\frac{1}{a}$=$-\frac{1}{{a}^{2}}(x-a)$.
整理得:x+a2y-2a=0.
取y=0,得:x=2a,取x=0,得y=$\frac{2}{a}$.
∴|AB|=$\sqrt{4{a}^{2}+\frac{4}{{a}^{2}}}$=2$\sqrt{{a}^{2}+\frac{1}{{a}^{2}}}$.
∴△OAB的周长为|2a|+|$\frac{2}{a}$|+2$\sqrt{{a}^{2}+\frac{1}{{a}^{2}}}$=2($a+\frac{1}{a}$)+2$\sqrt{{a}^{2}+\frac{1}{{a}^{2}}}$(a>0)
≥2×2a$•\frac{1}{a}$+2$\sqrt{2{a}^{2}•\frac{1}{{a}^{2}}}$=4+2$\sqrt{2}$.
当且仅当a=1时上式等号成立.
故答案为:$4+2\sqrt{2}$.
点评 本题考查了利用导数研究过曲线上某点的切线方程,考查了利用基本不等式求最值,是中档题.

练习册系列答案
相关题目
16.甲、乙两人各抛掷一次正方体骰子(六个面分别标有数字1,2,3,4,5,6),设甲、乙所抛掷骰子朝上的面的点数分别为x,y,则满足x>y的概率是( )
| A. | $\frac{1}{6}$ | B. | $\frac{5}{12}$ | C. | $\frac{7}{12}$ | D. | $\frac{1}{3}$ |
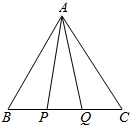 如图,在边长为6的正三角形△ABC内,△APQ的边PQ在BC边上滑动且PQ=2,求△APQ三边的平方和的最大值与最小值.
如图,在边长为6的正三角形△ABC内,△APQ的边PQ在BC边上滑动且PQ=2,求△APQ三边的平方和的最大值与最小值. 如图所示,一海轮在海上A处以每小时80海里的速度沿着南偏东40°的方向航行,这时观测到灯塔B在南偏东70°的方向上,航行1小时到达C处,在C处观测到灯塔B在北偏东65°方向上,问这时C到灯塔B的距离是多少?
如图所示,一海轮在海上A处以每小时80海里的速度沿着南偏东40°的方向航行,这时观测到灯塔B在南偏东70°的方向上,航行1小时到达C处,在C处观测到灯塔B在北偏东65°方向上,问这时C到灯塔B的距离是多少?