题目内容
【题目】平面直角坐标系![]() 中,直线
中,直线![]() 的参数方程是
的参数方程是![]() (
(![]() 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,以
为极点,以![]() 轴正半轴为极轴,建立极坐标系,曲线
轴正半轴为极轴,建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .将曲线
.将曲线![]() 上每一点的横坐标伸长到原来的两倍(纵坐标不变)得到曲线
上每一点的横坐标伸长到原来的两倍(纵坐标不变)得到曲线![]() .
.
(1)求曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)已知点![]() ,若直线
,若直线![]() 与曲线
与曲线![]() 交于
交于![]() ,
,![]() 两点,且
两点,且![]() ,求直线
,求直线![]() 的斜率.
的斜率.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
(1)利用极坐标公式将曲线![]() 的极坐标方程转化为直角坐标方程,再利用伸缩变换得到曲线
的极坐标方程转化为直角坐标方程,再利用伸缩变换得到曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)联立![]() 与
与![]() 的方程,利用直线参数方程的几何意义解决长度相关问题,求得直线
的方程,利用直线参数方程的几何意义解决长度相关问题,求得直线![]() 的斜率.
的斜率.
(1)![]() 的极坐标方程
的极坐标方程![]() 化为直角坐标方程为
化为直角坐标方程为![]() .
.
将曲线![]() 上每一点的横坐标伸长到原来的两倍(纵坐标不变)得到曲线
上每一点的横坐标伸长到原来的两倍(纵坐标不变)得到曲线![]() 的方程为
的方程为![]() .
.
(2)将![]() 的参数方程代入
的参数方程代入![]() 得
得![]() .
.
因为![]() 在圆
在圆![]() 内且在直线
内且在直线![]() 上,此方程一定有两个不等的实根,
上,此方程一定有两个不等的实根,
令![]() ,
,![]() 对应的参数为
对应的参数为![]() ,
,![]() ,则
,则![]() .
.
由韦达定理得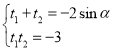 ,于是
,于是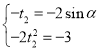 ,
,
消去![]() 得
得![]() ,得
,得![]() ,则斜率
,则斜率![]() .
.

 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
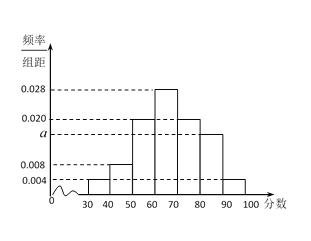
金状元绩优好卷系列答案【题目】改革开放40年,我国经济取得飞速发展,城市汽车保有量在不断增加,人们的交通安全意识也需要不断加强.为了解某城市不同性别驾驶员的交通安全意识,某小组利用假期进行一次全市驾驶员交通安全意识调查.随机抽取男女驾驶员各50人,进行问卷测评,所得分数的频率分布直方图如图所示.规定得分在80分以上为交通安全意识强.
安全意识强 | 安全意识不强 | 合计 | |
男性 | |||
女性 | |||
合计 |
(Ⅰ)求![]() 的值,并估计该城市驾驶员交通安全意识强的概率;
的值,并估计该城市驾驶员交通安全意识强的概率;
(Ⅱ)已知交通安全意识强的样本中男女比例为4:1,完成2×2列联表,并判断有多大把握认为交通安全意识与性别有关;
(Ⅲ)在(Ⅱ)的条件下,从交通安全意识强的驾驶员中随机抽取2人,求抽到的女性人数![]() 的分布列及期望.
的分布列及期望.
附: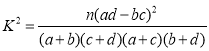 ,其中
,其中![]()
| 0.010 | 0.005 | 0.001 |
| 6.635 | 7.879 | 10.828 |
【题目】某工厂为了对新研发的一种产品进行合理定价,将该产品按事先拟定的价格进行试销,得到如下数据:
单价 | 8 | 8.2 | 8.4 | 8.6 | 8.8 | 9 |
销量 | 90 | 84 | 83 | 80 | 75 | 68 |
(1)若回归直线方程![]() ,其中
,其中![]() ;试预测当单价为10元时的销量;
;试预测当单价为10元时的销量;
(2)预计在今后的销售中,销量与单价仍然服从(1)中的关系,且该产品的成本是5元/件,为使工厂获得最大利润,该产品的单价应定为多少元?(利润=销售收入-成本)
【题目】2018以来,依托用户碎片化时间的娱乐需求、分享需求以及视频态的信息负载力,短视频快速崛起;与此同时,移动阅读方兴未艾,从侧面反应了人们对精神富足的一种追求,在习惯了大众娱乐所带来的短暂愉悦后,部分用户依旧对有着传统文学底蕴的严肃阅读青睐有加.某读书APP抽样调查了非一线城市![]() 和一线城市
和一线城市![]() 各100名用户的日使用时长(单位:分钟),绘制成频率分布直方图如下,其中日使用时长不低于60分钟的用户记为“活跃用户”.
各100名用户的日使用时长(单位:分钟),绘制成频率分布直方图如下,其中日使用时长不低于60分钟的用户记为“活跃用户”.
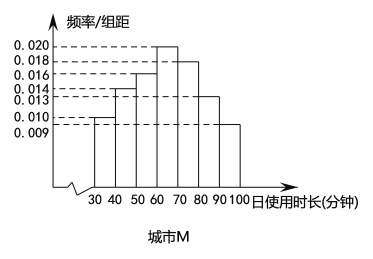
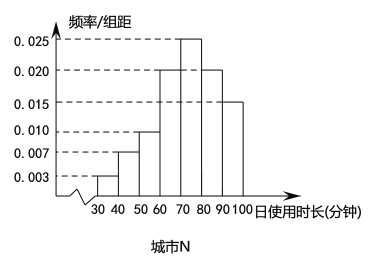
(1)请填写以下![]() 列联表,并判断是否有99%的把握认为用户活跃与否与所在城市有关?
列联表,并判断是否有99%的把握认为用户活跃与否与所在城市有关?
活跃用户 | 不活跃用户 | 合计 | |
城市 | |||
城市 | |||
合计 |
临界值表:
| 0.050 | 0.010 |
| 3.841 | 6.635 |
参考公式: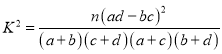 .
.
(2)以频率估计概率,从城市![]() 中任选2名用户,从城市
中任选2名用户,从城市![]() 中任选1名用户,设这3名用户中活跃用户的人数为
中任选1名用户,设这3名用户中活跃用户的人数为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
