Question

【题目】2018以来，依托用户碎片化时间的娱乐需求、分享需求以及视频态的信息负载力，短视频快速崛起；与此同时，移动阅读方兴未艾，从侧面反应了人们对精神富足的一种追求，在习惯了大众娱乐所带来的短暂愉悦后，部分用户依旧对有着传统文学底蕴的严肃阅读青睐有加.某读书APP抽样调查了非一线城市和一线城市各100名用户的日使用时长（单位：分钟），绘制成频率分布直方图如下，其中日使用时长不低于60分钟的用户记为“活跃用户”.

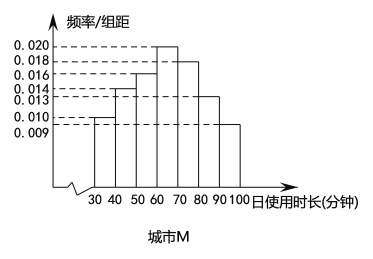
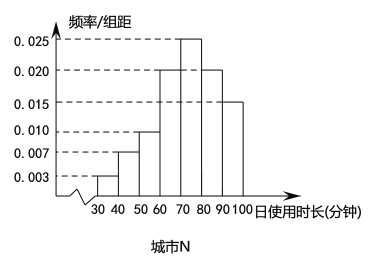
（1）请填写以下列联表，并判断是否有99%的把握认为用户活跃与否与所在城市有关？

	活跃用户	不活跃用户	合计
城市
城市
合计

临界值表：

	0.050	0.010
	3.841	6.635

参考公式：.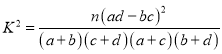

（2）以频率估计概率，从城市中任选2名用户，从城市中任选1名用户，设这3名用户中活跃用户的人数为，求的分布列和数学期望.

Answer 1

【答案】（1）填表见解析；有99%的把握认为用户是否活跃与所在城市有关；（2）分布列见解析；期望为2.

【解析】

（1）根据频率分布直方图分别求出城市、中的活跃用户与不活跃用户，即可得出列联表.

（2）由统计数据可知，城市中活跃用户占，城市N中活跃用户占，设从城市中任选的2名用户中活跃用户数为，，设从城市中任选的1名用户中活跃用户数为，服从两点分布，，利用二项分布求出概率即可得出分布列，再利用期望公式即可求解.

由已知可得以下列联表：

	活跃用户	不活跃用户	合计
城市	60	40	100
城市	80	20	100
合计	140	60	200

计算，

所以有99%的把握认为用户是否活跃与所在城市有关.

（2）由统计数据可知，城市中活跃用户占，城市N中活跃用户占，

设从城市中任选的2名用户中活跃用户数为，则

设从城市中任选的1名用户中活跃用户数为，则服从两点分布，

其中.故，

；

；

；

.

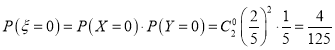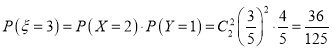故所求的分布列为

	0	1	2	3

.