题目内容
【题目】已知
,定点
,定直线
和
上的动点
满足：
在直线的同侧,点
在直线的另一侧.以为焦点作与直线相切的椭圆
,且当在上运动时,椭圆的长轴长为定值.
(1)求直线的方程；
(2)对于第一象限内任意2012个在椭圆上的点,是否一定可以将它们分成两组,使得其中一组点的横坐标之和不大于2013,另一组点的纵坐标之和不大于2013?请证明你的结论.
【答案】（1）
（2）见解析
【解析】
(1)设点
关于直线
的对称点为
.则
过椭圆与直线的切点.从而,
(即椭圆
的长轴长)为定值.于是,点Q在以为圆心、
为半径的圆上.
由
的任意性及在
上,知
.故点与
重合,即直线为线段
的中垂线.
注意到,
.
因为的中点为
,所以,直线的方程为.
(2)可以.
设这2012个点为
.
由(1)知直线的方程为.
又易知点
在直线
的下方,故
,且
.
不失一般性,不妨设
.
(i)若
,则将点
分为一组,点
作为一组符合题意.
(ii)若
,则存在
,使得
,且
.
于是,对任意的
,有
.
故
将点
分为一组,点
分为一组.则前一组点的横坐标之和不大于2013,后一组点的纵坐标之和不大于2013.
【题目】2022年北京冬奥运动会即第24届冬季奥林匹克运动会将在2022年2月4日至2月20日在北京和张家口举行，某研究机构为了了解大学生对冰壶运动的兴趣，随机从某大学生中抽取了120人进行调查，经统计男生与女生的人数比为11:13，男生中有30人表示对冰壶运动有兴趣，女生中有15人对冰壶运动没有兴趣.
（1）完成
列联表，并判断能否有99%的把握认为“对冰壶运动是否有兴趣与性别有关”？
有兴趣 | 没有兴趣 | 合计 | |
男 | 30 | ||
女 | 15 | ||
合计 | 120 |
（2）用分层抽样的方法从样本中对冰壶运动有兴趣的学生中抽取8人，求抽取的男生和女生分别为多少人？若从这8人中选取两人作为冰壶运动的宣传员，求选取的2人中恰好有1位男生和1位女生的概率.
附:
，其中n=a+b+c+d
P | 0.150 | 0.100 | 0.050 | 0.025 | 0.010 |
| 2.072 | 2.076 | 3.841 | 5.024 | 6.635 |
【题目】某知名电商在
双十一购物狂欢节中成交额再创新高，
月日单日成交额达
亿元.某店主在此次购物狂欢节期间开展了促销活动，为了解买家对此次促销活动的满意情况，随机抽取了参与活动的
位买家，调查了他们的年龄层次和购物满意情况，得到年龄层次的频率分布直方图和“购物评价为满意”的年龄层次频数分布表.年龄层次的频率分布直方图：
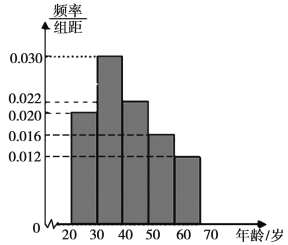
“购物评价为满意”的年龄层次频数分布表：
年龄（岁） |
|
|
|
|
|
频数 |
|
|
|
|
|
（1）估计参与此次活动的买家的平均年龄（同一组中的数据用该组区间的中点值做代表）；
（2）若年龄在
岁以下的称为“青年买家”，年龄在岁以上（含岁）的称为“中年买家”，完成下面的列联表，并判断能否有
的把握认为中、青年买家对此次活动的评价有差异？
评价满意 | 评价不满意 | 合计 | |
中年买家 | |||
青年买家 | |||
合计 |
|
附：参考公式：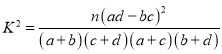
.
|
|
|
|
|
|
|
|
