题目内容
【题目】已知若干个长方体盒子,其棱长均为不大于正奇数![]() 的正整数(允许三棱长相同),且盒壁厚度忽略不计,每个盒子的三组对面分别染为红、蓝、黄三色,若没有一个盒子能以同色面平行的方式装入另一个盒子中,则称这些盒子是“和谐的”,求最多有多少个和谐盒子?
的正整数(允许三棱长相同),且盒壁厚度忽略不计,每个盒子的三组对面分别染为红、蓝、黄三色,若没有一个盒子能以同色面平行的方式装入另一个盒子中,则称这些盒子是“和谐的”,求最多有多少个和谐盒子?
【答案】![]()
【解析】
设和谐盒子最多有![]() 个,在空间直角坐标系中,坐标面
个,在空间直角坐标系中,坐标面![]() ,
,![]() ,
,![]() 分别染为红、蓝、黄三色,将上述盒子放入坐标系中,使其共顶点的三面分别放入同色的坐标面中,则每个盒子与一个整数有序数组
分别染为红、蓝、黄三色,将上述盒子放入坐标系中,使其共顶点的三面分别放入同色的坐标面中,则每个盒子与一个整数有序数组![]() 一一对应,其中,
一一对应,其中,![]() 、
、![]() 、
、![]() 、
、![]() ,
,![]() 、
、![]() 、
、![]() .从而,和谐盒子集合对应一个空间直角坐标系中的点集
.从而,和谐盒子集合对应一个空间直角坐标系中的点集![]() ,
,![]() ,满足对于任意
,满足对于任意![]() 中的两点
中的两点![]() ,
,![]() ,有
,有![]() , ①其中,
, ①其中,![]() .
.
设![]() ,其中,
,其中,![]() ,令
,令![]() ,
,![]() .显然,
.显然,![]() 中任意两点至多有一个分量相同,即
中任意两点至多有一个分量相同,即![]() ,且对任意
,且对任意![]() ,
,![]() ,有
,有![]() . ②
. ②
将![]() 中各元按
中各元按![]() 分量的大小排序,记为
分量的大小排序,记为![]() ,其中,
,其中,![]() .由式①知
.由式①知![]() .故
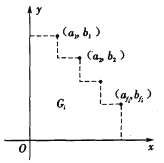
.故![]() ,如图,在
,如图,在![]() 坐标平面内记
坐标平面内记![]() ,
,![]() ,其中,
,其中,![]() ,
,![]() ,
,![]() ,
,![]() .从而,式②等价于
.从而,式②等价于![]() . ③
. ③
对于![]() ,若
,若![]() ,则将所有
,则将所有![]() 中的点并入
中的点并入![]() 中,将新集合记为
中,将新集合记为![]() ,则
,则![]() 仍满足式③,对
仍满足式③,对![]() 继续上述调整,直至
继续上述调整,直至![]() ,此时,仍记为
,此时,仍记为![]() ,将
,将![]() 各点依次连成一条折线,则所有
各点依次连成一条折线,则所有![]() 组成
组成![]() 中互不相交
中互不相交![]() 条折线,故
条折线,故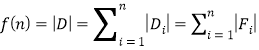
![]()
![]() ,当
,当![]() ,即
,即![]() 时,上式等号成立.
时,上式等号成立.
综上,和谐盒子至多有![]() 个.
个.

练习册系列答案
相关题目