题目内容
3．一列货车要在一定时间内行驶840千米，但行驶到一半时，被阻30分钟，为按时到达，必须每小时多行2千米，求行驶完全程原定时间是多少？分析 通过设原速度为x，利用时间关系$\frac{\frac{840}{2}}{x}$-$\frac{\frac{840}{2}}{x+2}$=$\frac{30}{60}$计算可得结论．
解答 解：设原速度为x，则有：$\frac{\frac{840}{2}}{x}$-$\frac{\frac{840}{2}}{x+2}$=$\frac{30}{60}$，
整理得：x2+2x-1680=0，
解得：x=40或x=-42（舍），
∴行驶完全程原定时间为$\frac{840}{40}$=21小时．
答：原计划时间21小时．
点评 本题考查函数模型的选择与应用，找出等量关系是解决本题的关键，注意解题方法的积累，属于基础题．
练习册系列答案
相关题目
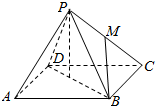已知四边形ABCD为正方形，P为面ABCD外一点，且PA=PB=PC=PD=2，AB=$\sqrt{2}$，M是侧棱PC的中点，则异面直线PA与BM所成的角的大小为45°．
11．
如图所示的是一个几何体的三视图，已知侧视图是一个等边三角形，根据图中尺寸可知这个几何体的表面积是（ ）
如图所示的是一个几何体的三视图，已知侧视图是一个等边三角形，根据图中尺寸可知这个几何体的表面积是（ ）| A． | 18+$\sqrt{3}$ | B． | $\frac{21\sqrt{3}}{2}$ | C． | 18+2$\sqrt{3}$ | D． | 6+2$\sqrt{3}$ |