题目内容
8.f(x)=$\frac{1}{3}$x3-$\frac{3}{2}$x2+ax+4的单调递减区间为[-1,4],求实数a取值范围.分析 求函数的导数,利用函数的单调性和导数之间的关系进行求解即可.
解答 解:函数的导数f′(x)=x2-3x+a,
∵f(x)=$\frac{1}{3}$x3-$\frac{3}{2}$x2+ax+4的单调递减区间为[-1,4],
∴f′(x)=x2-3x+a≤0的解集为[-1,4],
即-1,4是方程x2-3x+a=0的两个根,
则-1×4=a,
即a=-4.
点评 本题主要考查函数单调性和导数之间的关系,比较基础.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
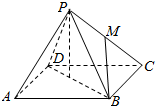 已知四边形ABCD为正方形,P为面ABCD外一点,且PA=PB=PC=PD=2,AB=$\sqrt{2}$,M是侧棱PC的中点,则异面直线PA与BM所成的角的大小为45°.
已知四边形ABCD为正方形,P为面ABCD外一点,且PA=PB=PC=PD=2,AB=$\sqrt{2}$,M是侧棱PC的中点,则异面直线PA与BM所成的角的大小为45°.