题目内容
若函数f（x）=2mx+4在[-2，1]上存在x0，使f（x0）=0，则实数m的取值范围（ ）
A．[-
| B．[-2，1] | C．[-1，2] | D．（-∞，-2]∪[1，+∞） |
由题意知m≠0，∴f（x）是单调函数，
又在[-2，1]上存在x0，使f（x0）=0，
∴f（-2）f（1）≤0，
即（-4m+4）（2m+4）≤0，解得m≤-2或m≥1．
故选：D．
又在[-2，1]上存在x0，使f（x0）=0，
∴f（-2）f（1）≤0，
即（-4m+4）（2m+4）≤0，解得m≤-2或m≥1．
故选：D．
练习册系列答案
相关题目
表示不超过实数
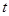的最大整数，则在坐标平面
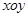上，满足
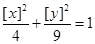的点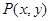
所形成的图形的面积为__________.
、
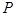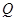满足条件：①
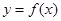的图像上；②
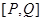是函数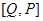
看作同一对“友好点对”）．已知函数
=
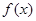，则此函数的“友好点对”有（ ）对．