题目内容
设函数f(x)=|x2-4x-5|.
(1)在区间[-2,6]上画出函数f(x)的图象;
(2)设集合A={x|f(x)≥5},B=(-∞,-2]∪[0,4]∪[6,+∞).试判断集合A和B之间的关系(要写出判断过程);
(3)当k>2时,求证:在区间[-1,5]上,y=kx+3k的图象位于函数f(x)图象的上方.
(1)在区间[-2,6]上画出函数f(x)的图象;
(2)设集合A={x|f(x)≥5},B=(-∞,-2]∪[0,4]∪[6,+∞).试判断集合A和B之间的关系(要写出判断过程);
(3)当k>2时,求证:在区间[-1,5]上,y=kx+3k的图象位于函数f(x)图象的上方.
(1)设-2≤x≤6,当x2-4x-5≥0时,
即6≥x≥5或-1≥x≥-2时,f(x)=x2-4x-5=(x-2)2-9
当x2-4x-5<0时,即-1<x<5时,f(x)=-(x2-4x-5)=-(x-2)2+9
故作图如下.
(2)方程f(x)=5的解分别是2-
,0,4
和2+
,由于f(x)在(-∞,-1]和[2,5]上单调递减,
在[-1,2]和[5,+∞)上单调递增,
∴A=(-∞,2-
]∪[0,4]∪[2+
,+∞).
由于2+
<6,2-
>-2
∴A?B.
(3)当x∈[-1,5]时,f(x)=-x2+4x+5.
g(x)=k(x+3)-(-x2+4x+5)=x2+(k-4)x+(3k-5)=(x-
)2-
,
∵k>2,∴
<1.又-1≤x≤5,
①当-1≤
<1,即2<k≤6时,
取x=
,g(x)min=-
=-
[(k-10)2-64].
∵16≤(k-10)2<64,
∴(k-10)2-64<0,则g(x)min>0.
②当
<-1,即k>6时,取x=-1,g(x)min=2k>0.
由①、②可知,当k>2时,g(x)>0,x∈[-1,5].
因此,在区间[-1,5]上,y=k(x+3)的图象位于函数f(x)图象的上方.
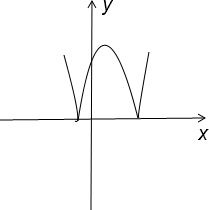
即6≥x≥5或-1≥x≥-2时,f(x)=x2-4x-5=(x-2)2-9
当x2-4x-5<0时,即-1<x<5时,f(x)=-(x2-4x-5)=-(x-2)2+9
故作图如下.
(2)方程f(x)=5的解分别是2-
| 14 |
和2+
| 14 |
在[-1,2]和[5,+∞)上单调递增,
∴A=(-∞,2-
| 14 |
| 14 |
由于2+
| 14 |
| 14 |
∴A?B.
(3)当x∈[-1,5]时,f(x)=-x2+4x+5.
g(x)=k(x+3)-(-x2+4x+5)=x2+(k-4)x+(3k-5)=(x-
| 4-k |
| 2 |
| k2-20k+36 |
| 4 |
∵k>2,∴
| 4-k |
| 2 |
①当-1≤
| 4-k |
| 2 |
取x=
| 4-k |
| 2 |
| k2-20k+36 |
| 4 |
| 1 |
| 4 |
∵16≤(k-10)2<64,
∴(k-10)2-64<0,则g(x)min>0.
②当
| 4-k |
| 2 |
由①、②可知,当k>2时,g(x)>0,x∈[-1,5].
因此,在区间[-1,5]上,y=k(x+3)的图象位于函数f(x)图象的上方.


练习册系列答案
相关题目
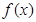 ,若存在区间
,若存在区间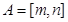 ,使得
,使得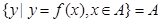 ,则称函数
,则称函数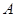 为函数
为函数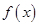 的一个“和谐区间”.给出下列4个函数:
的一个“和谐区间”.给出下列4个函数: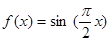 ;②
;②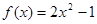 ;③
;③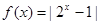 ; ④
; ④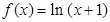 .
.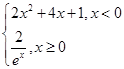 ,则f(x)的“友好点对”有________个.
,则f(x)的“友好点对”有________个.