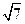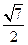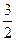题目内容
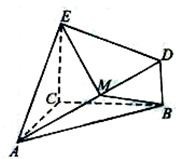
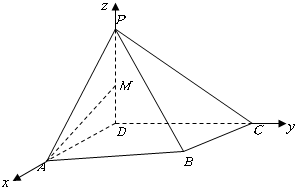
如图,四棱锥P-ABCD中,PD⊥底面ABCD,PD=DC=2AD,AD⊥DC,∠BCD=45°.
(1)设PD的中点为M,求证:AM∥平面PBC;
(2)求PA与平面PBC所成角的正弦值.
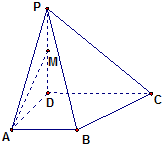
(1)设PD的中点为M,求证:AM∥平面PBC;
(2)求PA与平面PBC所成角的正弦值.

(1)证明:如图建立空间直角坐标系,设PD=CD=2AD=2,BC=
a,则A(1,0,0),B(a,2-a,0),C(0,2,0),P(0,0,2),M(0,0,1).…(3分)
设平面PBC的一个法向量为
=(x,y,z),则
•
=0,
•
=0
∴ax+y(2-a)-2z=0,2y-2z=0
令z=1得
=(1,1,1).…(7分)
而
=(-1,0,1),所以
•
=0,即
⊥
,
又AM?平面PBC
故AM∥平面PBC;.…(9分)
(2)
=(1,0,-2),设PA与平面PBC所成角为α,
由直线与平面所成角的向量公式有sinα=
=
=
. …(12分)
| 2 |
设平面PBC的一个法向量为
| n |
| n |
| PB |
| n |
| PC |
∴ax+y(2-a)-2z=0,2y-2z=0
令z=1得
| n |
而
| AM |
| AM |
| n |
| AM |
| n |
又AM?平面PBC
故AM∥平面PBC;.…(9分)
(2)
| PA |
由直线与平面所成角的向量公式有sinα=
|
| ||||
|
|
| 1 | ||||
|
| ||
| 15 |


练习册系列答案
相关题目