题目内容
正三棱锥的一个侧面的面积与底面积之比为2∶3,则这个三棱锥的侧面和底面所成二面角的度数为_________.
60°
设一个侧面面积为S1，底面面积为S，则这个侧面在底面上射影的面积为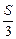
，由题设得
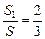，设侧面与底面所成二面角为θ,则cosθ=
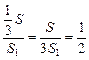,∴θ=60°.
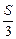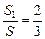，由题设得，设侧面与底面所成二面角为θ,则cosθ=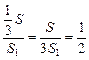,∴θ=60°. 
练习册系列答案
相关题目
题目内容
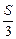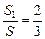，由题设得，设侧面与底面所成二面角为θ,则cosθ=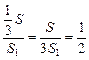,∴θ=60°. 
在平面
上的射影为正
，若
，
，
，求平面
与平面
所成锐二面角的大小．
=
=
，AB=CD=3，EF=
，求AB、CD所成角的大小.
沿对角线
折成直二面角，给出下列四个结论：①
；②
与
所成角为
；③
为正三角形；④
所成角为
分）如图，五面体
中
．底面
是正三角形，
．
四边形
是矩形
，
二面角
为直二面角．
在
上运动，当
∥平面
,并且
说明理由；
的
余弦值．
中，已知棱
的长为
，其余各棱长都为
，则二面角 
的余弦值为（ ）
