题目内容
【题目】如图,在直四棱柱ABCD﹣A1B1C1D1中,底面四边形ABCD是直角梯形,其中AB⊥AD,AB=BC=1且AD= ![]() AA1=2.
AA1=2. 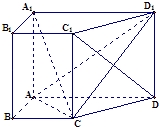
(1)求证:直线C1D⊥平面ACD1;
(2)试求三棱锥A1﹣ACD1的体积.
【答案】
(1)证明:在梯形ABCD内过C点作CE⊥AD交AD于点E,
则由底面四边形ABCD是直角梯形,AB⊥AD,AB=BC=1,
以及 ![]() 可得:CE=1,且
可得:CE=1,且 ![]() ,AC⊥CD.
,AC⊥CD.
又由题意知CC1⊥面ABCD,从而AC⊥CC1,而CC1∩CD=C,
故AC⊥C1D.
因CD=CC1,及已知可得CDD1C1是正方形,从而C1D⊥CD1.
因C1D⊥CD1,C1D⊥AC,且AC∩CD1=C,
所以C1D⊥面ACD1.
(2)解:因三棱锥A1﹣ACD1与三棱锥C﹣AA1D1是相同的,故只需求三棱锥C﹣AA1D1的体积即可,而CE⊥AD,
且由AA1⊥面ABCD可得CE⊥AA1,又因为AD∩AA1=A,
所以有CE⊥平面ADD1A1,即CE为三棱锥C﹣AA1D1的高.
故 ![]()
【解析】(1)通过证明C1D⊥CD1 , C1D⊥AC,说明AC与CD1是平面ACD1内的两条相交直线,利用直线与平面垂直的判定定理证明直线C1D⊥平面ACD1;(2)求三棱锥A1﹣ACD1的体积.转化为三棱锥C﹣AA1D1的体积,求出底面面积与高,即可求解棱锥的体积.
【考点精析】掌握直线与平面垂直的判定是解答本题的根本,需要知道一条直线与一个平面内的两条相交直线都垂直,则该直线与此平面垂直;注意点:a)定理中的“两条相交直线”这一条件不可忽视;b)定理体现了“直线与平面垂直”与“直线与直线垂直”互相转化的数学思想.

 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案【题目】某厂最近十年生产总量逐年上升,如表是部分统计数据:
年份 | 2008 | 2010 | 2012 | 2014 | 2016 |
生产总量(万吨) |
(Ⅰ)利用所给数据求年生产总量与年份之间的回归直线方程![]() ;
;
(Ⅱ)利用(Ⅰ)中所求出的直线方程预测该厂2018年生产总量.
(回归直线的方程: ![]() ,其中
,其中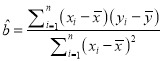 ,
, ![]() )
)