题目内容
【题目】设 
．
（1）用a表示f（x）的最大值M（a）；
（2）当M（a）=2时，求a的值．
【答案】
（1）解：f（x）= 
cos2x+asinx﹣ 
=﹣sin2x+asinx+ 
，
∵0≤x≤ 
∴0≤sinx≤1
令sinx=t，则g（t）=﹣t2+at+ ，t∈[0，1]
∴M（a）=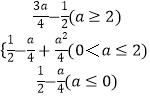 
（2）解：当M（a）=2时，
或a=﹣2（舍）； 
．
∴ 
或a=﹣6
【解析】（1）用二倍角公式对f（x）化简得f（x）=﹣sin2x+asinx+ ，设sinx=t，则函数g（t）是开口向下，对称轴为t= 
的抛物线，根据二次函数的性质，对a进行讨论得出答案．（2）M（a）=2代入（1）中的M（a）的表达式即可得出结果．
【考点精析】解答此题的关键在于理解三角函数的最值的相关知识，掌握函数
，当
时，取得最小值为
；当
时，取得最大值为
，则
，
，
．
练习册系列答案
应用题天天练四川大学出版社系列答案
相关题目
【题目】在平面直角坐标系
中，曲线
的参数方程为
（
为参数），在以原点为极点， 
轴正半轴为极轴的极坐标系中，直线
的极坐标方程为
．
（1）求曲线
的普通方程和直线
的倾斜角；
（2）设点
，直线
和曲线
交于
两点，求
的值．
【题目】某科技公司生产一种手机加密芯片，其质量按测试指标划分为：指标大于或等于
为合格品，小于为次品．现随机抽取这种芯片共
件进行检测，检测结果统计如表：
测试指标 |
|
|
|
|
|
芯片数量（件） |
|
|
|
|
|
已知生产一件芯片，若是合格品可盈利
元，若是次品则亏损
元.
（Ⅰ）试估计生产一件芯片为合格品的概率；并求生产
件芯片所获得的利润不少于
元的概率.
（Ⅱ）记
为生产
件芯片所得的总利润，求随机变量
的分布列和数学期望
