题目内容
【题目】已知等比数列{an}满足a1=2,a2=4(a3﹣a4),数列{bn}满足bn=3﹣2log2an .
(1)求数列{an}和{bn}的通项公式;
(2)令cn= ![]() ,求数列{cn}的前n项和Tn;
,求数列{cn}的前n项和Tn;
(3)若λ>0,求对所有的正整数n都有2λ2﹣kλ+2>a2nbn成立的k的范围.
【答案】
(1)解:设等比数列{an}的公比为q,
∵a1=2,a2=4(a3﹣a4),
∴ ![]() ,
,
故数列{an}是以2为首项, ![]() 为公比的等比数列,
为公比的等比数列,
∵ ![]() ,
,
∴数列{bn}是首项为1,公差为2的等差数列.
∴ ![]() ;
;
(2)解:∵cn= ![]() =(2n﹣1)2n﹣2,
=(2n﹣1)2n﹣2,
∴Tn= ![]() ×1+1×3+2×5+…+2n﹣2×(2n﹣1),
×1+1×3+2×5+…+2n﹣2×(2n﹣1),
![]() ,
,
两式相减得: ![]()
= ![]() ,
,
∴ ![]() ;
;
(3)解:由(1)知 ![]() ,
,
∴数列{a2nbn}为单调递减数列;
∴当n≥1时, ![]() ,即a2nbn最大值为1,
,即a2nbn最大值为1,
由2λ2﹣kλ+2>1可得 ![]() ,
,
而当λ>0时, ![]() ,当且仅当
,当且仅当 ![]() 时取等号,
时取等号,
∴ ![]() .
.
【解析】(1)通过设等比数列{an}的公比为q,通过a1=2、a2=4(a3﹣a4)计算可知数列{an}是以2为首项、 ![]() 为公比的等比数列,进而数列{bn}是首项为1、公差为2的等差数列,计算即得结论;(2)通过(1)可知cn=(2n﹣1)2n﹣2 , 利用错位相减法计算即得结论;(3)通过(1)知数列{a2nbn}为单调递减数列,进而只需解不等式2λ2﹣kλ+2>a2b1 , 利用基本不等式计算即得结论.
为公比的等比数列,进而数列{bn}是首项为1、公差为2的等差数列,计算即得结论;(2)通过(1)可知cn=(2n﹣1)2n﹣2 , 利用错位相减法计算即得结论;(3)通过(1)知数列{a2nbn}为单调递减数列,进而只需解不等式2λ2﹣kλ+2>a2b1 , 利用基本不等式计算即得结论.
【考点精析】根据题目的已知条件,利用等比数列的通项公式(及其变式)和数列的前n项和的相关知识可以得到问题的答案,需要掌握通项公式:![]() ;数列{an}的前n项和sn与通项an的关系
;数列{an}的前n项和sn与通项an的关系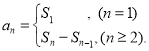 .
.

练习册系列答案
相关题目