题目内容
9.设全集U=R,函数f(x)=lg(|x+1|-1)的定义域为A,集合B={x|sinπx=0},则(∁UA)∩B的元素个数为( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 由对数式的真数大于0求得集合A,求解三角方程化简集合B,然后利用交、并、补集的混合运算得答案.
解答 解:由|x+1|-1>0,得|x+1|>1,即x<-2或x>0.
∴A={x|x<-2或x>0},则∁UA={x|-2≤x≤0};
由sinπx=0,得:πx=kπ,k∈Z,∴x=k,k∈Z.
则B={x|sinπx=0}={x|x=k,k∈Z},
则(∁UA)∩B={x|-2≤x≤0}∩{x|x=k,k∈Z}={-2,-1,0}.
∴(∁UA)∩B的元素个数为3.
故选:C.
点评 本题考查了交、并、补集的混合运算,考查了对数函数的定义域,考查了三角函数值的求法,是基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
14.已知{an}为等差数列,Sn为其前n项和.若a1=12,S6=S11,则必有( )
| A. | a17=0 | B. | a6+a12=0 | C. | S17>0 | D. | a9<0 |
18.已知集合A={x2-x-2>0},集合B={x||x-a|<3},若A∪B=R,则实数a的取值范围是( )
| A. | [1,2] | B. | (-1,2) | C. | [-1,2] | D. | (-2,1) |
 如图,已知切线PA切圆于点A,割线PBC分别交圆于点B,C,点D在线段BC上,且DC=2BD,∠BAD=∠PAB,$PA=2\sqrt{10}$,PB=4,则线段AB的长为2$\sqrt{3}$.
如图,已知切线PA切圆于点A,割线PBC分别交圆于点B,C,点D在线段BC上,且DC=2BD,∠BAD=∠PAB,$PA=2\sqrt{10}$,PB=4,则线段AB的长为2$\sqrt{3}$.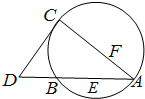 如图,CD为△ABC外接圆的切线,E,F分别为弦AB与弦AC上的点,AB的延长线交直线CD于点D,且BC•AE=DC•AF,B,E,F,C四点共圆.
如图,CD为△ABC外接圆的切线,E,F分别为弦AB与弦AC上的点,AB的延长线交直线CD于点D,且BC•AE=DC•AF,B,E,F,C四点共圆.