题目内容
20. 如图,已知切线PA切圆于点A,割线PBC分别交圆于点B,C,点D在线段BC上,且DC=2BD,∠BAD=∠PAB,$PA=2\sqrt{10}$,PB=4,则线段AB的长为2$\sqrt{3}$.
如图,已知切线PA切圆于点A,割线PBC分别交圆于点B,C,点D在线段BC上,且DC=2BD,∠BAD=∠PAB,$PA=2\sqrt{10}$,PB=4,则线段AB的长为2$\sqrt{3}$.
分析 利用切割线定理求出PC,可得BC,利用DC=2BD,可得BD=2,DC=4,证明△BCA∽△BAD,即可求出AB.
解答 解:因为切线PA切圆于点A,割线PBC分别交圆于点B,C,$PA=2\sqrt{10}$,PB=4,
所以40=4PC,
所以PC=10,
所以BC=6,
因为DC=2BD,
所以BD=2,DC=4,
因为∠BCA=∠PAB,∠BAD=∠PAB,
所以△BCA∽△BAD,
所以$\frac{BC}{BA}=\frac{BA}{BD}$,
所以BA=2$\sqrt{3}$.
故答案为:2$\sqrt{3}$.
点评 本题考查切割线定理,考查三角形相似的判断,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
5.已知实数x,y满足$\left\{\begin{array}{l}y≥1\\ y≤2x-1\\ x+y≤m\end{array}\right.$,如果目标函数z=x-y的最小值为-2,则实数m的值为( )
| A. | 0 | B. | 2 | C. | 4 | D. | 8 |
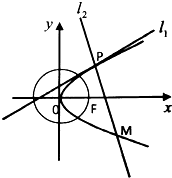 如图,已知圆O:x2+y2=a2(a>0)过抛物线C:y2=2px(p>0)的焦点F,过点F且与圆O相切的直线被抛物线C截得的弦长为4
如图,已知圆O:x2+y2=a2(a>0)过抛物线C:y2=2px(p>0)的焦点F,过点F且与圆O相切的直线被抛物线C截得的弦长为4