题目内容
2.已知$\overrightarrow{a},\overrightarrow{b}$是非零向量,f(x)=$(\overrightarrow{a}x-\overrightarrow{b})•(\overrightarrow{b}x-\overrightarrow{a})$.①若$\overrightarrow{a}⊥\overrightarrow{b}$,证明f(x)为奇函数
②若f(0)=3,f(x+2)=f(2-x),求|$\overrightarrow{a}+\overrightarrow{b}$|.
分析 ①化简$f(x)=({\overrightarrow ax-\overrightarrow b})({\overrightarrow bx-\overrightarrow a})=\overrightarrow a•\overrightarrow b{x^2}-({{{\overrightarrow a}^2}+{{\overrightarrow b}^2}})x+\overrightarrow a•\overrightarrow b$,从而可得$f(x)=-({{{\overrightarrow a}^2}+{{\overrightarrow b}^2}})x$,从而证明;
②由题意得$\overrightarrow{a}$•$\overrightarrow{b}$=3,-$\frac{-({\overrightarrow{a}}^{2}+{\overrightarrow{b}}^{2})}{2•\overrightarrow{a}•\overrightarrow{b}}$=2,从而解得.
解答 解:①∵$f(x)=({\overrightarrow ax-\overrightarrow b})({\overrightarrow bx-\overrightarrow a})=\overrightarrow a•\overrightarrow b{x^2}-({{{\overrightarrow a}^2}+{{\overrightarrow b}^2}})x+\overrightarrow a•\overrightarrow b$,
又∵$\overrightarrow{a}⊥\overrightarrow{b}$,
∴$\overrightarrow{a}$•$\overrightarrow{b}$=0,
∴$f(x)=-({{{\overrightarrow a}^2}+{{\overrightarrow b}^2}})x$,
故f(-x)=-(${\overrightarrow{a}}^{2}$+${\overrightarrow{b}}^{2}$)(-x)=-f(x),
故f(x)为奇函数.
②∵f(0)=3,
∴$\overrightarrow{a}$•$\overrightarrow{b}$=3,
∵f(x+2)=f(2-x),
∴函数f(x)的图象关于x=2对称,
故-$\frac{-({\overrightarrow{a}}^{2}+{\overrightarrow{b}}^{2})}{2•\overrightarrow{a}•\overrightarrow{b}}$=2,
故${\overrightarrow{a}}^{2}$+${\overrightarrow{b}}^{2}$=12,
故|$\overrightarrow{a}+\overrightarrow{b}$|=$\sqrt{{\overrightarrow{a}}^{2}+{\overrightarrow{b}}^{2}+2\overrightarrow{a}•\overrightarrow{b}}$=3$\sqrt{2}$.
点评 本题考查了平面向量的数量积的应用及函数的性质的判断与应用.

 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案 激活思维优加课堂系列答案
激活思维优加课堂系列答案| A. | {1,4} | B. | {1,3} | C. | {2,4} | D. | {2,3} |
| A. | a>b>c | B. | b>a>c | C. | a>c>b | D. | c>b>a |
| A. | f(x)=cos2x | B. | f(x)的最小正周期为π | ||
| C. | f(x)的图象关于直线x=0对称 | D. | f(x)的值域为[-$\sqrt{2}$,$\sqrt{2}$] |
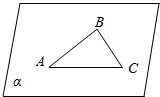 如图,在△ABC中,若AB,BC在平面α内,试判断AC是否在平面α内.
如图,在△ABC中,若AB,BC在平面α内,试判断AC是否在平面α内.