题目内容
10.对于函数y=f(x)与常数a,b,若f(2x)=af(x)+b恒成立,则称(a,b)为函数f(x)的一个“P数对”;设函数f(x)的定义域为R+,且f(1)=3.(Ⅰ)若(a,b)是f(x)的一个“P数对”,且f(2)=6,f(4)=9,求常数a,b的值;
(Ⅱ)若(-2,0)是f(x)的一个“P数对”,且当x∈[1,2)时f(x)=k-|2x-3|,求k的值及f(x)在区间[1,2n)(n∈N*)上的最大值与最小值.
分析 (Ⅰ)利用f(2)=6,f(4)=9,建立方程组,即可求常数a,b的值;
(Ⅱ)令x=1,则f(1)=k-1=3,解得k=4,当x∈[1,2)时f(x)=4-|2x-3|,得出f(x)在[1,2)上的取值范围是[3,4].利用由已知,f(2x)=-2f(x)恒成立,将[1,2n)分解成[2k-1,2k),(k∈N*)的并集,求出f(x)在各段[2k-1,2k)上的取值范围,各段上最大值、最小值即为所求的最大值,最小值.
解答 解:(Ⅰ)若(a,b)是f(x)的一个“P数对”,且f(2)=6,f(4)=9,
则f(2)=af(1)+b,即6=3a+b ①,
f(4)=af(2)+b,即9=6a+b,②,
解得a=1,b=3;
(Ⅱ)当x∈[1,2)时,f(x)=k-|2x-3|,
令x=1,可得f(1)=k-1=3,解得k=4,…10分
所以,x∈[1,2)时,f(x)=4-|2x-3|,
故f(x)在[1,2)上的取值范围是[3,4].
又(-2,0)是f(x)的一个“P数对”,故f(2x)=-2f(x)恒成立,
当x∈[2k-1,2k)(k∈N*)时,$\frac{x}{{{2^{k-1}}}}∈[1,2)$,$f(x)=-2f(\frac{x}{2})=4f(\frac{x}{4})$=…=${(-2)^{k-1}}f(\frac{x}{{{2^{k-1}}}})$,…9分
故k为奇数时,f(x)在[2k-1,2k)上的取值范围是[3×2k-1,2k+1];
当k为偶数时,f(x)在[2k-1,2k)上的取值范围是[-2k+1,-3×2k-1]. …11分
所以当n=1时,f(x)在[1,2n)上的最大值为4,最小值为3;
当n为不小于3的奇数时,f(x)在[1,2n)上的最大值为2n+1,最小值为-2n;
当n为不小于2的偶数时,f(x)在[1,2n)上的最大值为2n,最小值为-2n+1.…13分.
点评 本题考查利用新定义分析问题、解决问题的能力.考查转化计算,分类讨论、构造能力及推理论证能力,思维量大,属于难题.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案(1)定义域为R,值域为[1,+∞);
(2)图象关于x=2对称
(3)函数在(-∞,0)上是减函数
请写出函数f(x)的一个解析式(x-2)2+1(只要写出一个即可)
| A. | $[{0,\left.{\frac{π}{6}}]}\right.$ | B. | $[{0,\left.{\frac{π}{3}}]}\right.$ | C. | $[{0,\left.{\frac{π}{4}}]}\right.$ | D. | $[{\frac{π}{6},\left.{\frac{π}{4}}]}\right.$ |
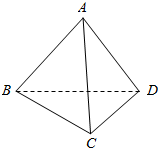 在空间四边形ABCD中,设AB⊥CD,AC⊥BD.
在空间四边形ABCD中,设AB⊥CD,AC⊥BD.