题目内容
【题目】如图,在平面直角坐标系![]() 中,已知
中,已知![]() 是椭圆
是椭圆![]() 上的一点,从原点
上的一点,从原点![]() 向圆
向圆![]() 作两条切线,分别交椭圆于点
作两条切线,分别交椭圆于点![]() .
.
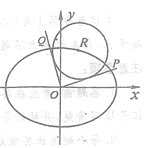
(1)若![]() 点在第一象限,且直线
点在第一象限,且直线![]() 互相垂直,求圆
互相垂直,求圆![]() 的方程;
的方程;
(2)若直线![]() 的斜率存在,并记为
的斜率存在,并记为![]() ,求
,求![]() 的值;
的值;
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
试题分析:本题主要考查椭圆的标准方程及其性质、直线与椭圆的位置关系、椭圆中的定值问题等基础知识,考查学生的分析问题解决问题的能力、转化能力、计算能力. 第一问,利用圆的半径、直线与圆相切,得到![]() ,结合点
,结合点![]() 在椭圆上,解出
在椭圆上,解出![]() ,从而得到圆
,从而得到圆![]() 的方程;第二问,由于直线与圆相切,圆心到直线的距离等于半径得到
的方程;第二问,由于直线与圆相切,圆心到直线的距离等于半径得到![]() ,再根据
,再根据![]() 解出
解出![]() 的值;
的值;
试题解析:(1)由圆![]() 的方程知圆
的方程知圆![]() 的半径
的半径![]() ,因为直线
,因为直线![]() 互相垂直,且和圆
互相垂直,且和圆![]() 相切,所以
相切,所以![]() ,即
,即
![]() ①
①
又点![]() 在椭圆
在椭圆![]() 上,所以
上,所以![]() ②
②
联立①②,解得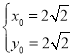 ,
,
所以,所求圆![]() 的方程为
的方程为
![]() .
.
(2)因为直线![]() 和
和![]() 都与圆
都与圆![]() 相切,所以
相切,所以 ,
,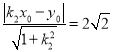 ,
,
化简得![]() ,
,
因为点![]() 在椭圆
在椭圆![]() 上,所以
上,所以![]() ,即
,即![]() ,
,
所以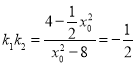 .
.

练习册系列答案
相关题目
【题目】某工厂生产部门随机抽测生产某种零件的工人的日加工零件数(单位:件),其中A车间13人,B车间12人,获得数据如下:

根据上述数据得到样本的频率分布表如下:
分组 | 频数 | 频率 |
[25,30] | 3 | 0.12 |
(30,35] | 5 | 0.20 |
(35,40] | 8 | 0.32 |
(40,45] | n1 | f1 |
(45,50] | n2 | f2 |
(1)确定样本频率分布表中n1、n2、f1和f2的值;
(2)现从日加工零件数落在(40,45]的工人中随机选取两个人,求这两个人中至少有一个来自B车间的概率.

