题目内容
【题目】已知椭圆![]() ,三点
,三点 中恰有二点在椭圆
中恰有二点在椭圆![]() 上,且离心率为
上,且离心率为![]() 。
。

(1)求椭圆![]() 的方程;
的方程;
(2)设![]() 为椭圆
为椭圆![]() 上任一点,
上任一点, ![]() 为椭圆
为椭圆![]() 的左右顶点,
的左右顶点, ![]() 为
为![]() 中点,求证:直线
中点,求证:直线![]() 与直线
与直线![]() 它们的斜率之积为定值;
它们的斜率之积为定值;
(3)若椭圆![]() 的右焦点为
的右焦点为![]() ,过
,过![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于
交于![]() ,求证:直线
,求证:直线![]() 与直线
与直线![]() 斜率之和为定值。
斜率之和为定值。
【答案】(1)![]() ;(2)见解析;(3)见解析.
;(2)见解析;(3)见解析.
【解析】试题分析:(1)先根据椭圆性质判断得![]() 在椭圆上,代入椭圆方程并与离心率联立解得
在椭圆上,代入椭圆方程并与离心率联立解得![]() (2)设
(2)设![]() ,用坐标表示
,用坐标表示![]() ,再根据点在椭圆上化简求值,(3)设
,再根据点在椭圆上化简求值,(3)设![]() ,用坐标表示
,用坐标表示![]() 联立直线方程与椭圆方程,利用韦达定理代人化简可得定值.
联立直线方程与椭圆方程,利用韦达定理代人化简可得定值.
试题解析:(1)由椭圆性质得: ![]()
在椭圆上, ![]()
得: ![]()
(2)设![]() 为椭圆上任一点,
为椭圆上任一点, ![]() ,
, ![]()
得: ![]()
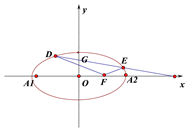
(3)设直线![]() :
: ![]() ,设
,设![]() 联立得:
联立得:
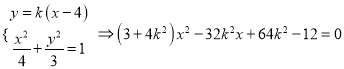
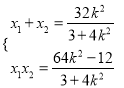 ,
, 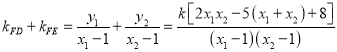
代入得, 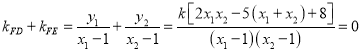

练习册系列答案
相关题目