题目内容

已知数列{an}是一个等差数列，且a2=1，a5=-5．
（1）求{an}的通项公式an和前n项和Sn；
（2）设Cn=
5-an
2
，bn=2cn求数列{bn}的前n项和Tn．
（1）设等差数列{an}的公差为d，
则d=
a5-a2
5-2
=-2，
∴an=a2+（n-2）d=-2n+5，
∴Sn=3n+
n(n-1)×(-2)
2
=4n-n2．
（2）∵Cn=
5-an
2
=n，
∴bn=2n，
bn+1
bn
=2（常数），
∴数列{bn}是首项为2，公比为2的等比数列，
∴Tn=
2(1-2n)
1-2
=2n+1-2．
练习册系列答案
相关题目
已知数列{an}的前n项和是sn=-
3
2
n2+
205
2
n，
（1）求数列的通项公式an；
（2）求数列{|an|}的前n项和．
已知数列{an}的各项均为正数，观察程序框图，若k=5，k=10时，分别有S=
5
11
和S=
10
21

（1）试求数列{an}的通项；
（2）令bn=2an，求b1+b2+…+bm的值．
已知Sn为数列{an}的前n项之和，a2=1，对任意的正整数n，都有Sn-2=p（an-2），其中p为常数，且p≠1．
（1）求p的值；（2）求Sn．
设数列{an}的前n项和为Sn，且Sn=4an+2n+1，n∈N*．
（1）求证：{an-2}是等比数列；
（2）求数列{nan}前n项和Tn．
已知二次函数y=f（x）的图象经过坐标原点，其导函数为f′（x）=6x-2，数列{an}的前n项和为Sn，点（n，Sn）（n∈N*）均在函数y=f（x）的图象上．
（Ⅰ）求数列{an}的通项公式；
（Ⅱ）设bn=
3
anan+1
，Tn是数列{bn}的前n项和，求使得Tn＜
m
20
对所有n∈N*都成立的最小正整数m．
在等比数列{an}中，Sn为{an}的前n项和，且S3=
7
2
，S6=
63
2
，
（1）求an．
（2）求数列{nan}的前n项和Tn．
已知数列{an}满足Sn=n2an（n∈N*），其中Sn是{an}的前n项和，且a1=1，求
（1）求an的表达式；
（2）求Sn．
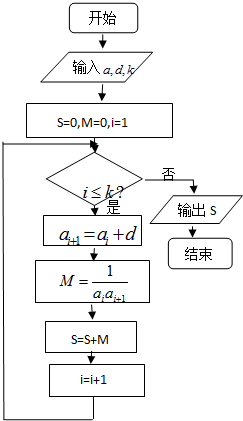
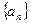数列的通项公式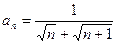，则该数列的前（　　）项之和等于.
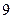A．B．C．D．.

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网