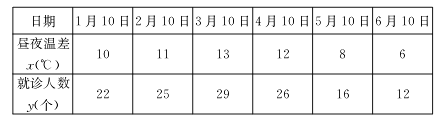
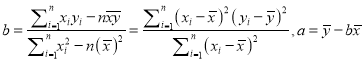ΧβΡΩΡΎ»ί
ΓΨΧβΡΩΓΩΡ≥ΒΊΖΫ’ΰΗ°“ΣΫΪ“ΜΩι»γΆΦΥυ ΨΒΡ÷±Ϋ«Χί–ΈABCDΩ’ΒΊΗΡΫ®ΈΣΫΓ…μ”ιά÷Ιψ≥Γ.“―÷ΣAD//BC, ![]() ΑΌΟΉΘ§
ΑΌΟΉΘ§ ![]() ΑΌΟΉΘ§Ιψ≥Γ»κΩΎP‘ΎAB…œΘ§«“
ΑΌΟΉΘ§Ιψ≥Γ»κΩΎP‘ΎAB…œΘ§«“![]() Θ§ΗυΨίΙφΜ°Θ§ΙΐΒψPΤΧ…ηΝΫΧθœύΜΞ¥Ι÷±ΒΡ± ÷±–Γ¬ΖPM,PNΘ®–Γ¬ΖΒΡΩμΕ»≤ΜΦΤΘ©Θ§ΒψM,NΖ÷±π‘Ύ±ΏAD,BC…œΘ®ΑϋΚ§ΕΥΒψΘ©Θ§
Θ§ΗυΨίΙφΜ°Θ§ΙΐΒψPΤΧ…ηΝΫΧθœύΜΞ¥Ι÷±ΒΡ± ÷±–Γ¬ΖPM,PNΘ®–Γ¬ΖΒΡΩμΕ»≤ΜΦΤΘ©Θ§ΒψM,NΖ÷±π‘Ύ±ΏAD,BC…œΘ®ΑϋΚ§ΕΥΒψΘ©Θ§![]() «χ”ρΡβΫ®ΈΣΧχΈηΫΓ…μΙψ≥ΓΘ§
«χ”ρΡβΫ®ΈΣΧχΈηΫΓ…μΙψ≥ΓΘ§ ![]() «χ”ρΡβΫ®ΈΣΕυΆ·ά÷‘ΑΘ§ΤδΥϋ«χ”ρΤΧ…η¬ΧΜ·≤ίΤΚΘ§…η
«χ”ρΡβΫ®ΈΣΕυΆ·ά÷‘ΑΘ§ΤδΥϋ«χ”ρΤΧ…η¬ΧΜ·≤ίΤΚΘ§…η![]() .
.
Θ®1Θ©«σ¬ΧΜ·≤ίΤΚΟφΜΐΒΡΉν¥σ÷ΒΘΜ
Θ®2Θ©œ÷ΡβΫΪΝΫΧθ–Γ¬ΖPNM,PNΫχ––≤ΜΆ§ΖγΗώΒΡΟάΜ·Θ§PM–Γ¬ΖΒΡΟάΜ·Ζ―”ΟΈΣΟΩΑΌΟΉ1Άρ‘ΣΘ§PN–Γ¬ΖΒΡΟάΜ·Ζ―”ΟΈΣΟΩΑΌΟΉ2Άρ‘ΣΘ§ ‘»ΖΕ®M,NΒΡΈΜ÷ΟΘ§ ΙΒΟ–Γ¬ΖPM,PNΒΡΟάΜ·ΉήΖ―”ΟΉνΒΆΘ§≤Δ«σ≥ωΉν–ΓΖ―”Ο.
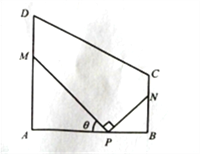
ΓΨ¥πΑΗΓΩ(1) ¬ΧΜ·≤ίΤΚΟφΜΐΒΡΉν¥σ÷ΒΈΣ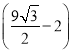 ΤΫΖΫΑΌΟΉ;(2)
ΤΫΖΫΑΌΟΉ;(2) ![]() ±ΉήΟάΜ·Ζ―”ΟΉνΒΆΈΣ4Άρ‘Σ.
±ΉήΟάΜ·Ζ―”ΟΉνΒΆΈΣ4Άρ‘Σ.
ΓΨΫβΈωΓΩ ‘ΧβΖ÷ΈωΘΚΘ®1Θ©œ»«σΒΟ![]()
![]() ,‘Όάϊ”ΟΨυ÷Β≤ΜΒ» Ϋ«σΒΟ’ΐΫβΘΜΘ®2Θ©œ»«σΒΟ
,‘Όάϊ”ΟΨυ÷Β≤ΜΒ» Ϋ«σΒΟ’ΐΫβΘΜΘ®2Θ©œ»«σΒΟ![]() Θ§
Θ§ ![]()
ΉήΟάΜ·Ζ―”ΟΈΣ![]() Θ§‘Όάϊ”ΟΒΦ ΐΙΛΨΏ«σΒΟ’ΐΫβ.
Θ§‘Όάϊ”ΟΒΦ ΐΙΛΨΏ«σΒΟ’ΐΫβ.
‘ΧβΫβΈωΘΚΘ®1Θ©‘Ύ![]() ÷–Θ§
÷–Θ§ ![]() Θ§ΒΟ
Θ§ΒΟ![]() Θ§
Θ§
Υυ“‘![]()
”…![]() ,
,![]()
‘Ύ![]() ÷–Θ§
÷–Θ§ ![]() Θ§ΒΟ
Θ§ΒΟ![]() Θ§
Θ§
Υυ“‘![]()
Υυ“‘¬ΧΜ·≤ίΤΚΟφΜΐ![]()
![]()
![]()
![]()
”÷“ρΈΣ![]()
Β±«“Β±![]() Θ§Φ¥
Θ§Φ¥![]() ΓΘ¥Υ ±
ΓΘ¥Υ ±![]()
Υυ“‘¬ΧΜ·≤ίΤΚΟφΜΐΒΡΉν¥σ÷ΒΈΣ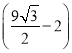 ΤΫΖΫΑΌΟΉ.
ΤΫΖΫΑΌΟΉ.
Θ®2Θ©ΖΫΖ®“ΜΘΚ‘Ύ![]() ÷–Θ§
÷–Θ§ ![]() Θ§ΒΟ
Θ§ΒΟ![]() Θ§
Θ§
”…![]() ,
,![]()
‘Ύ![]() ÷–Θ§
÷–Θ§ ![]() Θ§ΒΟ
Θ§ΒΟ![]() Θ§
Θ§
Υυ“‘ΉήΟάΜ·Ζ―”ΟΈΣ![]()
![]()
![]()
Νν![]() ΒΟ
ΒΟ![]() Ν–±μ»γœ¬
Ν–±μ»γœ¬
|
|
|
|
|
|
| - | 0 | - | ||
|
| ΒΞΒςΒίΦθ |
| ΒΞΒςΒί‘ω |
|
Υυ“‘Β±![]() ±Θ§Φ¥
±Θ§Φ¥![]() ±ΉήΟάΜ·Ζ―”ΟΉνΒΆΈΣ4Άρ‘ΣΓΘ
±ΉήΟάΜ·Ζ―”ΟΉνΒΆΈΣ4Άρ‘ΣΓΘ
ΖΫΖ®ΕΰΘΚ‘Ύ![]() ÷–Θ§
÷–Θ§ ![]() Θ§ΒΟ
Θ§ΒΟ![]() Θ§
Θ§
”…![]() ,
,![]()
‘Ύ![]() ÷–Θ§
÷–Θ§ ![]() Θ§ΒΟ
Θ§ΒΟ![]() Θ§
Θ§
Υυ“‘ΉήΟάΜ·Ζ―”ΟΈΣ![]()
![]()
Νν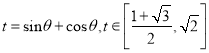 ΒΟ
ΒΟ![]()
Υυ“‘![]() Θ§
Θ§ 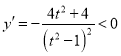
Υυ“‘![]() ‘Ύ
‘Ύ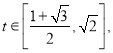 …œ «ΒΞΒςΒίΦθ
…œ «ΒΞΒςΒίΦθ
Υυ“‘Β±![]() Θ§
Θ§ ![]() ±Θ§Φ¥
±Θ§Φ¥![]() ±ΉήΟάΜ·Ζ―”ΟΉνΒΆΈΣ4Άρ‘ΣΓΘ
±ΉήΟάΜ·Ζ―”ΟΉνΒΆΈΣ4Άρ‘ΣΓΘ