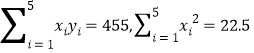题目内容
【题目】若定义在![]() 上的函数
上的函数![]() ,其图象是连续不断的,且存在常数
,其图象是连续不断的,且存在常数![]() 使得
使得![]() 对任意的实数
对任意的实数![]() 都成立,则称
都成立,则称![]() 是一个“
是一个“![]() 特征函数”则下列结论中正确的个数为( ).
特征函数”则下列结论中正确的个数为( ).
①![]() 是常数函数中唯一的“
是常数函数中唯一的“![]() 特征函数”;
特征函数”;
②![]() 不是“
不是“![]() 特征函数”;
特征函数”;
③“![]() 特征函数”至少有一个零点;
特征函数”至少有一个零点;
④![]() 是一个“
是一个“![]() 特征函数”;.
特征函数”;.
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】C
【解析】分析:利用新定义“![]() 特征函数”,逐个判断即可得到答案.
特征函数”,逐个判断即可得到答案.
详解:对于①设![]() 是一个“
是一个“![]() 特征函数”,则
特征函数”,则![]() ,当
,当![]() 时,可以取实数集,因此
时,可以取实数集,因此![]() 不是唯一一个常数“
不是唯一一个常数“![]() 特征函数”,故①错误;
特征函数”,故①错误;
对于②,∵![]() ,∴
,∴![]() ,即
,即![]() ,
,
∴当![]() 时,
时,![]() ;
;![]() 时,
时,![]() 有唯一解,
有唯一解,
∴不存在常数![]() 使得
使得![]() 对任意实数
对任意实数![]() 都成立,
都成立,
∴![]() 不是“
不是“![]() 特征函数”,故②正确;
特征函数”,故②正确;
对于③,令![]() 得
得![]() ,所以
,所以![]() ,
,
若![]() ,显然
,显然![]() 有实数根;若
有实数根;若![]() ,
,![]() .
.
又∵![]() 的函数图象是连续不断的,∴
的函数图象是连续不断的,∴![]() 在
在![]() 上必有实数根,
上必有实数根,
因此任意的“![]() 特征函数”必有根,即任意“
特征函数”必有根,即任意“![]() 特征函数”至少有一个零点,故③正确;
特征函数”至少有一个零点,故③正确;
对于④,假设![]() 是一个“
是一个“![]() 特征函数”,则
特征函数”,则![]() 对任意实数
对任意实数![]() 成立,则有
成立,则有![]() ,而此式有解,所以
,而此式有解,所以![]() 是“
是“![]() 特征函数”,故④正确.
特征函数”,故④正确.
综上所述,结论正确的是②③④,共![]() 个.
个.
故选![]() .
.

【题目】某兴趣小组欲研究昼夜温差大小与患感冒人数多少之间的关系,他们分别到气象局与某医院抄录了![]() 至
至![]() 月份每月
月份每月![]() 号的昼夜温差情况与因患感冒而就诊的人数,得到如下资料:
号的昼夜温差情况与因患感冒而就诊的人数,得到如下资料:
日期 | 1月10日 | 2月10日 | 3月10日 | 4月10日 | 5月10日 | 6月10日 |
昼夜温差
|
|
|
|
|
|
|
就诊人数 |
|
|
|
|
|
|
该兴趣小组确定的研究方案是:先从这六组数据中选取![]() 组,用剩下的
组,用剩下的![]() 组数据求线性回归方程,再用被选取的
组数据求线性回归方程,再用被选取的![]() 组数据进行检验.
组数据进行检验.
(1)求选取的![]() 组数据恰好是相邻两月的概率;
组数据恰好是相邻两月的概率;
(2)若选取的是1月与![]() 月的两组数据,请根据2至5月份的数据,求出
月的两组数据,请根据2至5月份的数据,求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(3)若由线性回归方程得到的估计数据与所选出的检验数据的误差均不超过![]() 人,则认为得到的线性回归方程是理想的,试问该小组所得线性回归方程是否理想?
人,则认为得到的线性回归方程是理想的,试问该小组所得线性回归方程是否理想?
参考数据![]() ,
,![]()
(参考公式:
 ,
,![]() )
)
【题目】网购已经成为一种时尚,商家为了鼓励消费,购买时在店铺领取优惠券,买后给予好评返还现金等促销手段.经统计,近五年某店铺用于促销的费用![]() (万元)与当年度该店铺的销售收人
(万元)与当年度该店铺的销售收人![]() (万元)的数据如下表:
(万元)的数据如下表:
年份 | 2013年 | 2014年 | 2015年 | 2016年 | 2017年 |
促销费用 |
|
|
|
|
|
销售收入 |
|
|
|
|
|
(1)请根据上表提供的数据,用最小二乘法求出/span>![]() 关于
关于![]() 的线性回归方
的线性回归方![]() ;
;
(2)2018年度该店铺预测销售收人至少达到![]() 万元,则该店铺至少准备投入多少万元的促销费?
万元,则该店铺至少准备投入多少万元的促销费?
参考公式: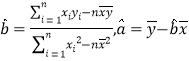
参考数据: