题目内容
在四边形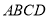 中,对角线
中,对角线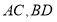 垂直相交于点
垂直相交于点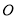 ,且
,且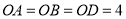 ,
,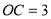 .将
.将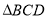 沿
沿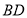 折到
折到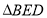 的位置,使得二面角
的位置,使得二面角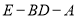 的大小为
的大小为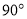 (如图).已知
(如图).已知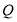 为
为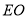 的中点,点
的中点,点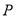 在线段
在线段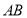 上,且
上,且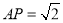 .
.
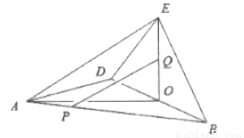
(1)证明:直线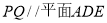 ;
;
(2)求直线 与平面
与平面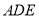 所成角
所成角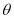 的正弦值.
的正弦值.
练习册系列答案
相关题目
题目内容
在四边形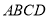 中,对角线
中,对角线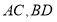 垂直相交于点
垂直相交于点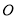 ,且
,且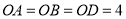 ,
,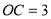 .将
.将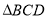 沿
沿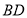 折到
折到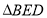 的位置,使得二面角
的位置,使得二面角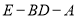 的大小为
的大小为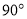 (如图).已知
(如图).已知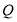 为
为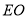 的中点,点
的中点,点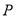 在线段
在线段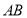 上,且
上,且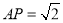 .
.

(1)证明:直线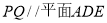 ;
;
(2)求直线 与平面
与平面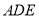 所成角
所成角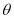 的正弦值.
的正弦值.