题目内容
【题目】定义区间![]() ,
,![]() ,
,![]() ,
,![]() 的长度为
的长度为![]() .如果一个函数的所有单调递增区间的长度之和为
.如果一个函数的所有单调递增区间的长度之和为![]() (其中
(其中![]() ,
,![]() 为自然对数的底数),那么称这个函数为“
为自然对数的底数),那么称这个函数为“![]() 函数”.下列四个命题:
函数”.下列四个命题:
①函数![]() 不是“
不是“![]() 函数”;
函数”;
②函数![]() 是“
是“![]() 函数”,且
函数”,且![]() ;
;
③函数![]() 是“
是“![]() 函数”;
函数”;
④函数![]() 是“
是“![]() 函数”,且
函数”,且![]() .
.
其中正确的命题的个数为( )
A. 4个B. 3个C. 2个D. 1个
【答案】B
【解析】
利用导数、函数的图象,对四个命题逐一判断出真假。
分析命题①: ![]() 定义域为
定义域为![]() ,
,![]() ,
,
![]() ,
,![]() 函数
函数![]() 在
在![]() 上是单调递增,显然这个区间没有长度,因此函数
上是单调递增,显然这个区间没有长度,因此函数![]() 不是“
不是“![]() 函数”,故命题①是真命题。
函数”,故命题①是真命题。
分析命题②:![]() ,定义域为
,定义域为![]() ,
, ![]()
当![]() 时,函数
时,函数![]() 是增函数,
是增函数,![]()
![]()
![]()
构造两个函数,![]() ,图象如下图所示:
,图象如下图所示:

通过图象可知当![]() ,
,![]() 而
而![]() ,即
,即![]() ,
, ![]() ,所以当
,所以当![]() 时,函数
时,函数![]() 是增函数,增区间的长度为
是增函数,增区间的长度为![]() ,又因为
,又因为![]() 显然有
显然有![]() 成立,所以函数
成立,所以函数![]() 是“m函数”,
是“m函数”,![]()
![]()
![]()
![]() 即
即![]() 成立,故命题②是真命题。
成立,故命题②是真命题。
分析命题③: 函数![]() 定义域为
定义域为![]() ,
,![]()
显然![]() 时,
时,![]() ,此时函数
,此时函数![]() 是单调递增函数,增区间为
是单调递增函数,增区间为![]() ,而区间
,而区间![]() 没有长度,故函数
没有长度,故函数![]() 不是“
不是“![]() 函数”,故命题③是假命题。
函数”,故命题③是假命题。
分析命题④:函数![]() 定义域
定义域![]() ,
,![]()
当![]() 时,
时,![]() 是增函数,故只需
是增函数,故只需![]() 成立,
成立,![]() 是增函数,
是增函数,
也就是![]() 成立,
成立,![]() 是增函数,构造二个函数,
是增函数,构造二个函数,![]() 如下图所示:
如下图所示:
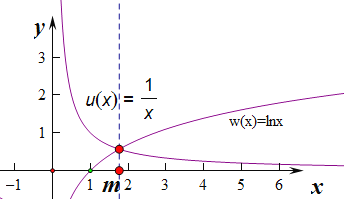
通过图象可知:当![]() 时,
时,![]() ,而
,而![]() ,所以
,所以![]() 。从而有
。从而有![]() 时,
时,![]() 时,函数
时,函数![]() 是增函数,显然区间
是增函数,显然区间![]() 长度为
长度为![]() ,而
,而![]()
所以函数![]() 是“
是“![]() 函数”,又
函数”,又![]() ,即
,即![]() 。故命题④是真命题。
。故命题④是真命题。
综上所述:正确的命题的个数为3个,故本题选B。

练习册系列答案
相关题目