题目内容
18.已知平面向量$\overrightarrow{a}$=(2,4),$\overrightarrow b=({1,-2})$,若$\overrightarrow c=\overrightarrow a-({\overrightarrow a•\overrightarrow b})\overrightarrow b$,则|$\overrightarrow{c}$|=8$\sqrt{2}$.分析 由已知求出$\overrightarrow{c}$的坐标,然后进行模的计算.
解答 解:$\overrightarrow a•\overrightarrow b=2-8=-6$,
∴$({\overrightarrow a•\overrightarrow b})•\overrightarrow b=({-6,12})$,
∴$\overrightarrow c=\overrightarrow a-({-6,12})=({8,-8})$,
∴$|{\overrightarrow c}|=\sqrt{{8^2}+{{({-8})}^2}}=8\sqrt{2}$
故答案为:8$\sqrt{2}$.
点评 本题考查了平面向量的坐标运算以及向量模的求法;属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
9.三位男生和一位女生并排照相,若女生不排在两端,则不同的排法共有( )
| A. | 6种 | B. | 12种 | C. | 18种 | D. | 24种 |
6.命题p1:△ABC所在平面内一点G满足$\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}=\overrightarrow{0}$,则G是△ABC的重心;命题p2:已知a为实数,则a>1是$\frac{1}{a}$<1的必要不充分条件,则下列命题为真命题的是( )
| A. | p1∧p2 | B. | ¬p1∧p2 | C. | ¬p1∨p2 | D. | p1∨p2 |
13.执行如图所示的程序框图,若输入x的值为2+log23,则输出y的值为( )
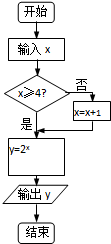

| A. | $\frac{8}{3}$ | B. | 8 | C. | 12 | D. | 24 |
6. 为了让学生了解环保,增强环保意识,某中学举行了一次环保知识竞赛,共有900名学生参加了这次竞赛.为了了解本次竞赛的成绩情况,从中抽取了部分学生的成绩(得分取正整数,满分为100分)进行统计.请你根据下面尚未完成的频率分布表和频率分布直方图,解答下列问题:
为了让学生了解环保,增强环保意识,某中学举行了一次环保知识竞赛,共有900名学生参加了这次竞赛.为了了解本次竞赛的成绩情况,从中抽取了部分学生的成绩(得分取正整数,满分为100分)进行统计.请你根据下面尚未完成的频率分布表和频率分布直方图,解答下列问题:
(1)填充频率分布表中的空格;
(2)不具体计算频率/组距,补全频率分布直方图.
 为了让学生了解环保,增强环保意识,某中学举行了一次环保知识竞赛,共有900名学生参加了这次竞赛.为了了解本次竞赛的成绩情况,从中抽取了部分学生的成绩(得分取正整数,满分为100分)进行统计.请你根据下面尚未完成的频率分布表和频率分布直方图,解答下列问题:
为了让学生了解环保,增强环保意识,某中学举行了一次环保知识竞赛,共有900名学生参加了这次竞赛.为了了解本次竞赛的成绩情况,从中抽取了部分学生的成绩(得分取正整数,满分为100分)进行统计.请你根据下面尚未完成的频率分布表和频率分布直方图,解答下列问题:| 分组 | 频数 | 频率 |
| [50,60) | 4 | 0.08 |
| [60,70) | 8 | 0.16 |
| [70,80) | 10 | 0.20 |
| [80,90) | 16 | 0.32 |
| [90,100] | ||
| 合计 |
(2)不具体计算频率/组距,补全频率分布直方图.
3.已知圆C1:(x-1)2+y2=2和圆C2:(x-3)2+(y-2)2=r2恰好有3条公切线,则圆C2的周长为( )
| A. | π | B. | $\sqrt{2}$π | C. | 2$\sqrt{2}$π | D. | 4π |