题目内容
4.设⊙E与⊙F相离,过E向⊙F作切线交⊙E于A、B,过F向⊙E作切线交⊙F于C、D,求证:AB=CD.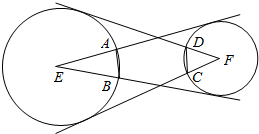
分析 取⊙E与⊙F上的两个切点PQ,连接QE,PF,EF,根据切线的性质,分别求出AB,CD,可得结论.
解答 证明:取⊙E与⊙F上的两个切点PQ,连接QE,PF,EF,如下图所示: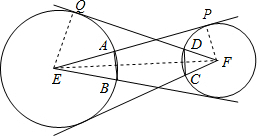
根据切线的性质,可得EQ⊥FQ,CD⊥EF,
则$\frac{EQ}{EF}=\frac{\frac{1}{2}CD}{FD}$,即CD=$\frac{2EQ•FD}{EF}$,
同理可得:AB=$\frac{2EQ•FD}{EF}$,
故AB=CD
点评 本题考查的知识点是圆的切线的性质定理,与圆相关的比例线段,难度不大,属于基础题.

练习册系列答案
相关题目
15.在等差数列{an}的前n项和为Sn,若a1,a2,S3成等比数列,则$\frac{{S}_{n}}{n{a}_{n}}$等于( )
| A. | $\frac{n}{2n-1}$ | B. | $\frac{n}{2n+1}$ | C. | $\frac{2n-1}{n}$ | D. | $\frac{2n+1}{n}$ |
19.设a=sin33°,b=cos58°,c=tan34°,则( )
| A. | a>b>c | B. | b>c>a | C. | c>b>a | D. | c>a>b |
13.设a=sin 17°cos45°+cos17°sin45°,b=1-2sin213°,c=$\frac{\sqrt{3}}{2}$,则有( )
| A. | c<a<b | B. | b<c<a | C. | a<b<c | D. | b<a<c |