题目内容
3.已知圆C1:(x-1)2+y2=2和圆C2:(x-3)2+(y-2)2=r2恰好有3条公切线,则圆C2的周长为( )| A. | π | B. | $\sqrt{2}$π | C. | 2$\sqrt{2}$π | D. | 4π |
分析 根据圆C1与圆C2恰好有3条公切线,得出两圆外切,从而求出圆C2的半径,即可求出周长.
解答 解:圆C1:(x-1)2+y2=2和圆C2:(x-3)2+(y-2)2=r2恰好有3条公切线,
∴圆C1与圆C2外切,
∴两圆的圆心距为d=R+r
∴$\sqrt{{(1-3)}^{2}{+(0-2)}^{2}}$=$\sqrt{2}$+r
∴r=$\sqrt{2}$,
∴圆C2的周长为2πr=2$\sqrt{2}$π.
故答案为:C.
点评 本题考查了两圆的位置关系的应用问题,也考查了求圆周长的应用问题,是基础题目.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
8.已知复数z=(a-2)+ai(a∈R,i为虚数单位)为纯虚数,则${∫}_{0}^{a}$$\sqrt{4-{x}^{2}}$dx的值为( )
| A. | π | B. | $\frac{π}{2}$ | C. | 2 | D. | 4 |
15.在等差数列{an}的前n项和为Sn,若a1,a2,S3成等比数列,则$\frac{{S}_{n}}{n{a}_{n}}$等于( )
| A. | $\frac{n}{2n-1}$ | B. | $\frac{n}{2n+1}$ | C. | $\frac{2n-1}{n}$ | D. | $\frac{2n+1}{n}$ |
13.设a=sin 17°cos45°+cos17°sin45°,b=1-2sin213°,c=$\frac{\sqrt{3}}{2}$,则有( )
| A. | c<a<b | B. | b<c<a | C. | a<b<c | D. | b<a<c |
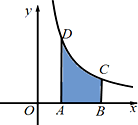 如图,曲边梯形ABCD由直线x=1,x=e,x轴及曲线y=$\frac{3}{x}$围成,则这个曲边梯形的面积是3.(注:e为自然对数的底数)
如图,曲边梯形ABCD由直线x=1,x=e,x轴及曲线y=$\frac{3}{x}$围成,则这个曲边梯形的面积是3.(注:e为自然对数的底数) 如图,O是矩形A1A2A3A4的中心,B1,B2,C1,C2分别是矩形四条边的中点,A1A2=4,A2A3=2$\sqrt{3}$,若以B1B2所在直线为x轴,O为坐标原点建立平面直角坐标系,记以O为对称中心,同时经过点C2,B2的椭圆为W.
如图,O是矩形A1A2A3A4的中心,B1,B2,C1,C2分别是矩形四条边的中点,A1A2=4,A2A3=2$\sqrt{3}$,若以B1B2所在直线为x轴,O为坐标原点建立平面直角坐标系,记以O为对称中心,同时经过点C2,B2的椭圆为W.