题目内容
【题目】成书于公元一世纪的我国经典数学著作《九章算术》中有这样一道名题,就是“引葭赴岸”问题,题目是:“今有池方一丈,点生其中央,出水一尺,引葭赶岸,适马岸齐,问水深,葭长各几何?”题意是:有一正方形池塘,边长为一丈(10尺),有棵芦苇长在它的正中央,高出水面部分有1尺长,把芦苇拉向岸边,恰好碰到沿岸(池塘一边的中点),则水深为__________尺,芦苇长__________尺.
【答案】12 13
【解析】
把问题转化为如图的数学几何图形,根据题意,可知EB′的长为10尺,则B′C=5尺,设出AB=AB′=x尺,表示出水深AC,根据勾股定理建立方程,求出方程的解即可得到芦苇的长和水深.
依题意画出图形,设芦苇长AB=AB′=x尺,
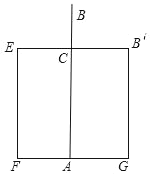
则水深AC=(x1)尺,
∵B′E=10尺,∴B′C=5尺,
在Rt△AB′C中,52+(x1)2=x2,
解得x=13(尺),
∴水深为12尺,芦苇长为13尺.
故答案为:12,13.

练习册系列答案
相关题目