题目内容
【题目】已知:椭圆![]() 的离心率为
的离心率为![]() ,且
,且![]() ,过左焦点
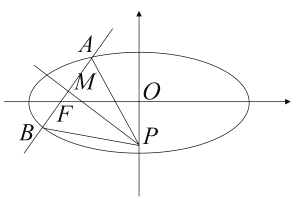
,过左焦点![]() 作一条直线交椭圆于
作一条直线交椭圆于![]() 、
、![]() 两点,过线段
两点,过线段![]() 的中点
的中点![]() 作
作![]() 的垂线交
的垂线交![]() 轴于点
轴于点![]() .
.
(1)求椭圆方程;
(2)当![]() 面积最大时,求直线
面积最大时,求直线![]() 的斜率.
的斜率.
【答案】(1)![]() (2)
(2)![]()
【解析】
(1)根据离心率为![]() ,且a+b=3,a2=b2+c2可求椭圆方程;
,且a+b=3,a2=b2+c2可求椭圆方程;
(2)设出直线AB方程![]() ,利用韦达定理求出
,利用韦达定理求出![]() 及中点M坐标,从而可得直线MP方程
及中点M坐标,从而可得直线MP方程![]() ,求出P点坐标,再利用点到直线距离公式写出面积,根据导数求最值.
,求出P点坐标,再利用点到直线距离公式写出面积,根据导数求最值.
(1)由已知条件可得,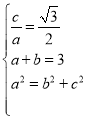 ,化简解得a=2,b=1,c=
,化简解得a=2,b=1,c=![]()
∴椭圆方程为![]() ;
;
(2)设![]() ,
,![]() ,与椭圆联立消去x,
,与椭圆联立消去x,
得:![]() ,
,
![]() ,
,
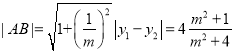 ,
,
又![]() ,
,
中点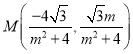 ,所以
,所以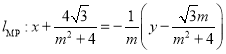 ,
,
令x=0,可得![]() ,
,
故得点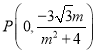 ,到
,到![]() 的距离
的距离![]() ,
,
所以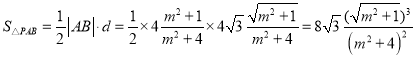 ,
,
令![]() ,则
,则 ,
,
构造函数![]() ,
,![]() ,
,
可得![]()
![]()
即![]() 时
时![]() 取得最小值,
取得最小值,
所以![]() 即
即![]() 时,
时,![]() 面积最大.
面积最大.
当![]() 面积最大时,直线
面积最大时,直线![]() 的斜率为
的斜率为![]() .
.

 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案【题目】近年来,随着国家综合国力的提升和科技的进步,截至![]() 年底,中国铁路运营里程达
年底,中国铁路运营里程达![]() 万千米,这个数字比
万千米,这个数字比![]() 年增长了
年增长了![]() 倍;高铁运营里程突破
倍;高铁运营里程突破![]() 万千米,占世界高铁运营里程的
万千米,占世界高铁运营里程的![]() 以上,居世界第一位.如表截取了
以上,居世界第一位.如表截取了![]() 年中国高铁密度的发展情况(单位:千米/万平方千米).
年中国高铁密度的发展情况(单位:千米/万平方千米).
年份 |
|
|
|
|
|
年份代码 |
|
|
|
|
|
高铁密度 |
|
|
|
|
|
已知高铁密度![]() 与年份代码
与年份代码![]() 之间满足关系式
之间满足关系式![]() (
(![]() 为大于
为大于![]() 的常数).
的常数).
(1)根据所给数据,求![]() 关于
关于![]() 的回归方程(精确到
的回归方程(精确到![]() 位);
位);
(2)利用(1)的结论,预测到哪一年,高铁密度会超过![]() 千米/万平方千米.
千米/万平方千米.
参考公式:设具有线性相关系的两个变量![]() 的一组数据为
的一组数据为![]() ,则回归方程
,则回归方程![]() 的系数:
的系数: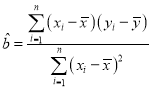 ,
,![]()
参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
【题目】某土特产超市为预估2020年元旦期间游客购买土特产的情况,对2019年元旦期间的90位游客购买情况进行统计,得到如下人数分布表.
购买金额(元) |
|
|
|
|
|
|
人数 | 10 | 15 | 20 | 15 | 20 | 10 |
(1)根据以上数据完成![]() 列联表,并判断是否有
列联表,并判断是否有![]() 的把握认为购买金额是否少于60元与性别有关.
的把握认为购买金额是否少于60元与性别有关.
不少于60元 | 少于60元 | 合计 | |
男 | 40 | ||
18 | |||
合计 |
(2)为吸引游客,该超市推出一种优惠方案,购买金额不少于60元可抽奖3次,每次中奖概率为![]() (每次抽奖互不影响,且
(每次抽奖互不影响,且![]() 的值等于人数分布表中购买金额不少于60元的频率),中奖1次减5元,中奖2次减10元,中奖3次减15元.若游客甲计划购买80元的土特产,请列出实际付款数
的值等于人数分布表中购买金额不少于60元的频率),中奖1次减5元,中奖2次减10元,中奖3次减15元.若游客甲计划购买80元的土特产,请列出实际付款数![]() (元)的分布列并求其数学期望.
(元)的分布列并求其数学期望.
附:参考公式和数据: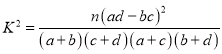 ,
,![]() .
.
附表:
| 2.072 | 2.706 | 3.841 | 6.635 | 7.879 |
| 0.150 | 0.100 | 0.050 | 0.010 | 0.005 |