题目内容
12.已知函数f(x)=ax-$\frac{2}{x}$-3lnx,其中a为常数.(1)当函数f(x)的图象在点($\frac{2}{3}$,f($\frac{2}{3}$))处的切线的斜率为1时,求函数f(x)在[$\frac{3}{2}$,3]上最小值;
(2)若函数f(x)在区间(0,+∞)上既有极大值又有极小值,求a的取值范围.
分析 (1)求出导数f′(x),由题意和导数的几何意义列出关于a的方程,解出a代入f′(x)化简,由导数的符号可求得函数的极小值,同时也为最小值;
(2)先化简f′(x),将条件转化为:“f′(x)=0有两个不等正实根“,再根据两根之和、两根之积大于0及判别式符号可得不等式组,求出a的取值范围.
解答 解:(1)由题意得,$f′(x)=a+\frac{2}{{x}^{2}}-\frac{3}{x}$,
因为f(x)的图象在点($\frac{2}{3}$,f($\frac{2}{3}$))处的切线的斜率为1,
所以$f′(\frac{2}{3})=1$,解得a=1,
则$f′(x)=1+\frac{2}{{x}^{2}}-\frac{3}{x}$=$\frac{{x}^{2}-3x+2}{{x}^{2}}$=$\frac{(x-1)(x-2)}{{x}^{2}}$,
所以当$\frac{3}{2}≤x$<2时,f′(x)<0,当2<x≤3时,f′(x)>0,
则x=2是f(x)的极小值点,也是最小值点,
所以f(x)min=f(2)=1-3ln2;
(2)$f′(x)=a+\frac{2}{{x}^{2}}-\frac{3}{x}$=$\frac{{ax}^{2}-3x+2}{{x}^{2}}$,
因为f(x)在(0,+∞)上既有极大值也有极小值,
所以f′(x)=0即ax2-3x+2=0有两个不等的正实根,
不妨设这两个正实根为x1、x2,并令h(x)=ax2-3x+2,
则$\left\{\begin{array}{l}{△=9-8a>0}\\{\frac{3}{a}>0}\\{\frac{2}{a}>0}\end{array}\right.$,解得0$<a<\frac{9}{8}$,
所以a的取值范围是(0,$\frac{9}{8}$).
点评 本题考查导数的几何意义,利用导数研究函数的极值,以及二次方程根的问题,考查了转化思想和分析解决问题的能力.

| A. | 若m⊥n,则α⊥β | B. | 若m∥n,则α⊥β | C. | 若m⊥n,则α∥β | D. | 若m∥n,则α∥β |
 如图,四棱锥P-ABCD,底面ABCD为正方形,PA=PD,PA⊥平面PDC,E为棱PD的中点
如图,四棱锥P-ABCD,底面ABCD为正方形,PA=PD,PA⊥平面PDC,E为棱PD的中点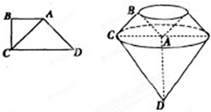 已知梯形ABCD中,AB∥CD,∠B=$\frac{π}{2}$,DC=2AB=2BC=2$\sqrt{2}$,以直线AD为旋转轴旋转一周的都如图所示的几何体
已知梯形ABCD中,AB∥CD,∠B=$\frac{π}{2}$,DC=2AB=2BC=2$\sqrt{2}$,以直线AD为旋转轴旋转一周的都如图所示的几何体 如图,在多面体ABCDEF中,矩形ADEF与梯形ABCD所在的平面互相垂直,AD⊥CD,AB∥CD,AB=AD=2,CD=4,M为CE的中点,N为CD的中点.
如图,在多面体ABCDEF中,矩形ADEF与梯形ABCD所在的平面互相垂直,AD⊥CD,AB∥CD,AB=AD=2,CD=4,M为CE的中点,N为CD的中点.