题目内容
17.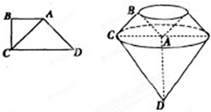 已知梯形ABCD中,AB∥CD,∠B=$\frac{π}{2}$,DC=2AB=2BC=2$\sqrt{2}$,以直线AD为旋转轴旋转一周的都如图所示的几何体
已知梯形ABCD中,AB∥CD,∠B=$\frac{π}{2}$,DC=2AB=2BC=2$\sqrt{2}$,以直线AD为旋转轴旋转一周的都如图所示的几何体(Ⅰ)求几何体的表面积
(Ⅱ)判断在圆A上是否存在点M,使二面角M-BC-D的大小为45°,且∠CAM为锐角若存在,请求出CM的弦长,若不存在,请说明理由.
分析 (1)根据题意知该旋转体下半部分是一个圆锥,上半部分是一个圆台中间挖空一个圆锥而剩下的几何体,求出它的表面积即可;
(2)作ME⊥AC,EF⊥BC,连结FM,说明∠MFE为二面角M-BC-D的平面角,设∠CAM=θ,通过tan∠MFE=1求出$sin\frac{θ}{2}=\frac{1}{\sqrt{3}}$,然后求解CM.
解答  解:(1)根据题意,得;
解:(1)根据题意,得;
该旋转体的下半部分是一个圆锥,
上半部分是一个圆台中间挖空一个圆锥而剩下的几何体,
其表面积为S=$\frac{1}{2}$×4π×2$\sqrt{2}$×2=8$\sqrt{2}$π,
或S=$\frac{1}{2}$×4π×2$\sqrt{2}$+$\frac{1}{2}$×(4π×2$\sqrt{2}$-2π×$\sqrt{2}$)+$\frac{1}{2}$×2π×$\sqrt{2}$=8$\sqrt{2}$π;
(2)作ME⊥AC,EF⊥BC,连结FM,易证FM⊥BC,
∴∠MFE为二面角M-BC-D的平面角,
设∠CAM=θ,∴
EM=2sinθ,EF=$\sqrt{2}(1-cosθ)$,
∵tan∠MFE=1,∴$\frac{2sinθ}{\sqrt{2}(1-cosθ)}=1$,∴tan$\frac{θ}{2}$=$\frac{\sqrt{2}}{2}$,∴$sin\frac{θ}{2}=\frac{1}{\sqrt{3}}$,
∴CM=2$•2sin\frac{θ}{2}=\frac{4\sqrt{3}}{3}$.
点评 本题考查了空间几何体的表面积与体积的计算问题,也考查了空间想象能力的应用问题,是综合性题目.

练习册系列答案
 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案
相关题目
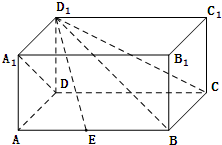 在四棱柱ABCD-A1B1C1D1中,侧棱DD1⊥底面ABCD,底面ABCD是矩形,且AD=AA1.
在四棱柱ABCD-A1B1C1D1中,侧棱DD1⊥底面ABCD,底面ABCD是矩形,且AD=AA1. 如图,正方体ABCD-A1B1C1D1中,E,F分别是AB,BC的中点.求证:
如图,正方体ABCD-A1B1C1D1中,E,F分别是AB,BC的中点.求证: 如图,在△ABC中,CD是∠ACB的角平分线,△ADC的外接圆交BC于点E,AB=2AC=6,EC=6,则AD的长为$\frac{3}{2}$.
如图,在△ABC中,CD是∠ACB的角平分线,△ADC的外接圆交BC于点E,AB=2AC=6,EC=6,则AD的长为$\frac{3}{2}$.