题目内容
20．设m，n是不同的直线，α，β是不同的平面，已知m∥α，n⊥β，下列说法正确的是（ ）| A． | 若m⊥n，则α⊥β | B． | 若m∥n，则α⊥β | C． | 若m⊥n，则α∥β | D． | 若m∥n，则α∥β |
分析 乘法利用空间线面平行和面面平行的判定定理和性质定理对选项分别分析选择．
解答 解：由已知m∥α，n⊥β，
对于A，若m⊥n，则α、β可能平行；如图
对于B，若m∥n，得到m⊥β由面面垂直的判定定理可得α⊥β；故B正确；
对于C，若m⊥n，则α、β有可能相交；如图
对于D，若m∥n，则m⊥β，由线面垂直的性质以及面面垂直的判定定理可得，α⊥β；故D错误．
故选B
点评 本题考查了空间线面平行和面面平行面面垂直的判定定理和性质定理的运用；关键是正确掌握定理的条件，充分发挥空间想象能力．
练习册系列答案
相关题目
5．
某市为了节约能源，拟出台“阶梯电价”制度，即制定住户月用电量的临界值a，若某住户某月用电量不超过a度，则按平价计费；若某月用电量超过a度，则超出部分按议价计费．未超出分布按平价计费．为确定a的值，随机调查了该市100户的月用电量，工作人员已将90户的用电量填在了下面的频率分布表中，最后10户的月用电量（单位：度）为：18 63 43 119 65 77 29 97 52 100
（Ⅰ）完成频率分布表并绘制频率分布直方图；
（Ⅱ）根据已有信息，试估计全市住户的平均用电量（同一组数据用该区间的中点值作代表）；
（Ⅲ）若该市计划让全市75%的住户在“阶梯电价”出台前后缴纳的电费不变，试求临界值a．
某市为了节约能源，拟出台“阶梯电价”制度，即制定住户月用电量的临界值a，若某住户某月用电量不超过a度，则按平价计费；若某月用电量超过a度，则超出部分按议价计费．未超出分布按平价计费．为确定a的值，随机调查了该市100户的月用电量，工作人员已将90户的用电量填在了下面的频率分布表中，最后10户的月用电量（单位：度）为：18 63 43 119 65 77 29 97 52 100| 组别 | 月用电量 | 频数统计 | 频数 | 频率 |
| 1 | [0，20） |  | ||
| 2 | [20，40） | 正正一 | ||
| 3 | [40，60） | 正正正正 | ||
| 4 | [60，80） | 正正正正正 | ||
| 5 | [80，100） | 正正正正 | ||
| 6 | [100，120） |  |
（Ⅱ）根据已有信息，试估计全市住户的平均用电量（同一组数据用该区间的中点值作代表）；
（Ⅲ）若该市计划让全市75%的住户在“阶梯电价”出台前后缴纳的电费不变，试求临界值a．
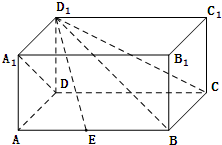在四棱柱ABCD-A1B1C1D1中，侧棱DD1⊥底面ABCD，底面ABCD是矩形，且AD=AA1．
如图，在△ABC中，CD是∠ACB的角平分线，△ADC的外接圆交BC于点E，AB=2AC=6，EC=6，则AD的长为$\frac{3}{2}$．