题目内容
【题目】已知椭圆C:![]() +
+![]() =1(a>b>0)的离心率为
=1(a>b>0)的离心率为![]() ,F为椭圆C的右焦点,A是右准线与x轴的交点,且AF=1.
,F为椭圆C的右焦点,A是右准线与x轴的交点,且AF=1.

(1)求椭圆C的方程;
(2)过椭圆C上顶点B的直线l交椭圆另一点D,交x轴于点M,若![]() ,求直线l的方程;
,求直线l的方程;
(3)设点![]() ,过点F且斜率不为零的直线m与椭圆C交于S,T两点,直线TQ与直线x=2交于点S1,试问
,过点F且斜率不为零的直线m与椭圆C交于S,T两点,直线TQ与直线x=2交于点S1,试问![]() 是否为定值?若是,求出这个定值,若不是,请说明理由.
是否为定值?若是,求出这个定值,若不是,请说明理由.
【答案】(1)![]() ;(2)
;(2)![]() ,或
,或![]() ;(3)定值为0,理由见解析
;(3)定值为0,理由见解析
【解析】
(1)由![]() ,得到
,得到![]() ,再由离心率,即可求出
,再由离心率,即可求出![]() 、
、![]() 和
和![]() ,然后写出椭圆方程即可;
,然后写出椭圆方程即可;
(2)由点![]() 坐标设直线方程
坐标设直线方程![]() ,求出点
,求出点![]() 坐标,再由直线方程代入椭圆方程,利用韦达定理,求解出点
坐标,再由直线方程代入椭圆方程,利用韦达定理,求解出点![]() 横坐标,再根据
横坐标,再根据![]() ,求出
,求出![]() ,即可得到直线
,即可得到直线![]() 的方程;
的方程;
(3)设直线![]() 的方程
的方程![]() ,代入椭圆方程,利用韦达定理,表示出
,代入椭圆方程,利用韦达定理,表示出![]() 和
和![]() ;再利用点
;再利用点![]() 和点
和点![]() 设直线
设直线![]() 方程,求出点
方程,求出点![]() ,即可求出
,即可求出![]() 为定值.
为定值.
(1)由题意,椭圆右准线方程:![]() ,点
,点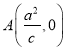 ,焦点
,焦点![]() ,
,
因为![]() ,所以
,所以![]() ,又
,又![]() ,
,
解得,![]() ,
,![]() ,所以
,所以![]() ,
,
所以椭圆方程为:![]() ;
;
(2)由(1)知,点![]() ,所以设直线
,所以设直线![]() 方程:
方程:![]() ,
,
![]() 时,
时,![]() ,所以点
,所以点![]() ,
,
直线方程代入椭圆方程并整理得,![]() ,
,
设点![]() ,由韦达定理,
,由韦达定理,![]() ,
,
![]() ,
,![]() ,
,
又![]() ,所以
,所以![]() ,解得
,解得![]() ,
,
所以直线![]() :
:![]() ,或
,或![]() ;
;
(3)由(1)知,点![]() ,点
,点![]() ,所以设直线
,所以设直线![]() :
:![]() ,
,
代入椭圆方程并整理得,![]() ,
,
设点![]() ,点
,点![]() ,
,
由韦达定理,![]() ,
,![]() ,
,
所以![]() ,
,
设直线![]() :
: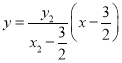 ,
,
当![]() 时,
时, ,
,
又![]() ,
,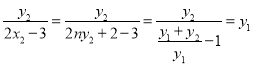 ,
,
所以点![]() ,
,![]() ,
,![]() ,
,
![]() ,即
,即![]() 为定值,定值为
为定值,定值为![]() .
.

 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
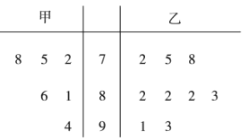
名校名卷单元同步训练测试题系列答案【题目】某高三理科班共有![]() 名同学参加某次考试,从中随机挑出
名同学参加某次考试,从中随机挑出![]() 名同学,他们的数学成绩
名同学,他们的数学成绩![]() 与物理成绩
与物理成绩![]() 如下表:
如下表:
数学成绩 |
|
|
|
|
|
物理成绩 |
|
|
|
|
|
(1)数据表明![]() 与
与![]() 之间有较强的线性关系,求
之间有较强的线性关系,求![]() 关于
关于![]() 的线性回归方程;
的线性回归方程;
(2)本次考试中,规定数学成绩达到![]() 分为优秀,物理成绩达到
分为优秀,物理成绩达到![]() 分为优秀.若该班数学优秀率与物理优秀率分别为
分为优秀.若该班数学优秀率与物理优秀率分别为![]() 和
和![]() ,且除去抽走的
,且除去抽走的![]() 名同学外,剩下的同学中数学优秀但物理不优秀的同学共有
名同学外,剩下的同学中数学优秀但物理不优秀的同学共有![]() 人,请写出
人,请写出![]() 列联表,判断能否在犯错误的概率不超过
列联表,判断能否在犯错误的概率不超过![]() 的前提下认为数学优秀与物理优秀有关?
的前提下认为数学优秀与物理优秀有关?
参考数据: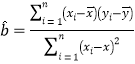 ,
,![]() ;
;![]() ,
,![]() ;
;![]()
【题目】某媒体对“男女延迟退休″这一公众关注的问题进行名意调查,如表是在某单位得到的数据:
赞同 | 反对 | 合计 | |
男 | 50 | 150 | 200 |
女 | 30 | 170 | 200 |
合计 | 80 | 320 | 400 |
(I)能否有97.5%的把握认为对这一问题的看法与性别有关?
(II)从赞同“男女延迟退休”的80人中,利用分层抽样的方法抽出8人,然后从中选出3人进行陈述发言,设发言的女士人数为X,求X的分布列和期望.
参考公式:![]()
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |