题目内容
【题目】△ABC中,sin(A﹣B)=sinC﹣sinB,D是边BC的一个三等分点(靠近点B),记 ![]() ,则当λ取最大值时,tan∠ACD= .
,则当λ取最大值时,tan∠ACD= .
【答案】2+ ![]()
【解析】解:∵sin(A﹣B)=sinC﹣sinB, ∴sinAcosB﹣cosAsinB=sinC﹣sinB=sinAcosB+cosAsinB﹣sinB,
∴sinB=2cosAsinB,∵sinB≠0,
∴cosA= ![]() ,由A∈(0,π),可得:A=
,由A∈(0,π),可得:A= ![]() ,
,
在△ADB中,由正弦定理可将 ![]() ,变形为则
,变形为则 ![]() ,
,
∵ ![]() =
= ![]()
∴ ![]() 即a2λ2=4c2+b2+2bc…①
即a2λ2=4c2+b2+2bc…①
在△ACB中,由余弦定理得:a2=b2+c2﹣bc…②
由①②得 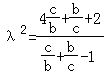
令 ![]() ,
, 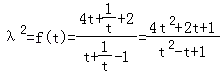 ,f′(t)=
,f′(t)= ![]() ,令f′(t)=0,得t=
,令f′(t)=0,得t= ![]() ,
,
即 ![]() 时,λ最大.
时,λ最大.
结合②可得b= ![]() ,a=
,a= ![]() c
c
在△ACB中,由正弦定理得 ![]()
![]() ,tanC=2+
,tanC=2+ ![]()
所以答案是:2+ ![]() .
.
【考点精析】通过灵活运用正弦定理的定义,掌握正弦定理:![]() 即可以解答此题.
即可以解答此题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】随着国家二孩政策的全面放开,为了调查一线城市和非一线城市的二孩生育意愿,某机构用简单随机抽样方法从不同地区调查了100位育龄妇女,结果如表.
非一线 | 一线 | 总计 | |
愿生 | 45 | 20 | 65 |
不愿生 | 13 | 22 | 35 |
总计 | 58 | 42 | 100 |
附表:
P(K2≥k) | 0.050 | 0.010 | 0.001 |
k | 3.841 | 6.635 | 10.828 |
由K2= ![]() 算得,K2=
算得,K2= ![]() ≈9.616参照附表,得到的正确结论是( )
≈9.616参照附表,得到的正确结论是( )
A.在犯错误的概率不超过0.1%的前提下,认为“生育意愿与城市级别有关”
B.在犯错误的概率不超过0.1%的前提下,认为“生育意愿与城市级别无关”
C.有99%以上的把握认为“生育意愿与城市级别有关”
D.有99%以上的把握认为“生育意愿与城市级别无关”