Question

【题目】已知直线C1 （t为参数），C2 （θ为参数），
（Ⅰ）当α= 时，求C1与C2的交点坐标；
（Ⅱ）过坐标原点O做C1的垂线，垂足为A，P为OA中点，当α变化时，求P点的轨迹的参数方程，并指出它是什么曲线．

Answer 1

【答案】解：（Ⅰ）当α= 时，C1的普通方程为 ，C2的普通方程为x2+y2=1．

联立方程组 ，

解得C1与C2的交点为（1，0） ．

（Ⅱ）C1的普通方程为xsinα-ycosα-sinα=0①．

则OA的方程为xcosα+ysinα=0②，

联立①②可得x=sin2α，y=-cosαsinα；

A点坐标为（sin2α，-cosαsinα），

故当α变化时，P点轨迹的参数方程为：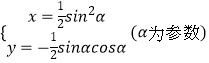

P点轨迹的普通方程 ．

故P点轨迹是圆心为 ，半径为 的圆

【解析】(1)根据题意结合已知条件求出直线的方程再联立直线与圆的方程即可求出交点的坐标。(2)首先联立两个方程求出点A的坐标由角的变化得出点P的参数方程再根据极坐标和直角坐标的互化关系得出圆的标准方程进而求出圆心坐标以及半径。