题目内容
【题目】在平面直角坐标系xOy中,已知圆![]() ,三个点
,三个点![]() ,B、C均在圆
,B、C均在圆![]() 上,
上,
(1)求该圆的圆心![]() 的坐标;
的坐标;
(2)若![]() ,求直线BC的方程;
,求直线BC的方程;
(3)设点![]() 满足四边形TABC是平行四边形,求实数t的取值范围.
满足四边形TABC是平行四边形,求实数t的取值范围.
【答案】(1)![]() (2)
(2)![]() 或
或![]() (3)
(3)![]() ,
,![]()
【解析】
(1)将![]() 点代入圆的方程可得
点代入圆的方程可得![]() 的值,继而求出半径和圆心(2)可设直线
的值,继而求出半径和圆心(2)可设直线![]() 方程为:
方程为:![]() ,可得圆心
,可得圆心![]() 到直线
到直线![]() 的距离,结合弦心距定理可得
的距离,结合弦心距定理可得![]() 的值,求出直线方程(3)设
的值,求出直线方程(3)设![]() ,
,![]() ,
,![]() ,
,![]() ,因为平行四边形的对角线互相平分,得
,因为平行四边形的对角线互相平分,得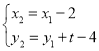 ,
,![]() ,于是点
,于是点![]() 既在圆
既在圆![]() 上,又在圆
上,又在圆![]() 上,从而圆
上,从而圆![]() 与圆
与圆![]() 上有公共点,即可求解.
上有公共点,即可求解.
(1)将![]() 代入圆
代入圆![]()
得![]() ,
,
解得![]() ,
,
![]() .半径
.半径![]() .
.
(2)![]()
![]() ,
,
![]() ,且
,且![]() ,
,
设直线![]() ,即
,即![]() ,
,
圆心![]() 到直线
到直线![]() 的距离
的距离![]() ,
,
由勾股定理得![]() ,
,
![]() ,
,
![]()
![]() ,
,
![]() ,
,
![]() 或
或![]() ,
,
所以直线![]() 的方程为
的方程为![]() 或
或![]() .
.
(3)设![]() ,
,![]() ,
,![]() ,
,![]() ,
,
因为平行四边形的对角线互相平分,
所以 ①,
①,
因为点![]() 在圆
在圆![]() 上,
上,
所以![]() ②
②
将①代入②,得
![]() ,
,
于是点![]() 既在圆
既在圆![]() 上,又在圆
上,又在圆![]() 上,
上,
从而圆![]() 与圆
与圆![]() 有公共点,
有公共点,
所以![]() ,
,
解得![]() .
.
因此,实数![]() 的取值范围是
的取值范围是![]() ,
,![]() .
.

练习册系列答案
相关题目
【题目】某种产品的质量以其质量指标值来衡量,质量指标值越大表明质量越好,记其质量指标值为![]() ,当
,当![]() 时,产品为一等品;当
时,产品为一等品;当![]() 时,产品为二等品;当
时,产品为二等品;当![]() 时,产品为三等品.现有甲、乙两条生产线,各生产了100件该产品,测量每件产品的质量指标值,得到下面的试验结果.(以下均视频率为概率)
时,产品为三等品.现有甲、乙两条生产线,各生产了100件该产品,测量每件产品的质量指标值,得到下面的试验结果.(以下均视频率为概率)
甲生产线生产的产品的质量指标值的频数分布表:
指标值分组 |
|
|
|
|
频数 | 10 | 30 | 40 | 20 |
乙生产线产生的产品的质量指标值的频数分布表:
指标值分组 |
|
|
|
|
|
频数 | 10 | 15 | 25 | 30 | 20 |
(1)若从乙生产线生产的产品中有放回地随机抽取3件,求至少抽到2件三等品的概率;
(2)若该产品的利润率![]() 与质量指标值
与质量指标值![]() 满足关系:
满足关系: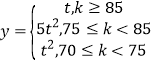 ,其中
,其中![]() ,从长期来看,哪条生产线生产的产品的平均利润率更高?请说明理由.
,从长期来看,哪条生产线生产的产品的平均利润率更高?请说明理由.