题目内容
【题目】已知函数f(x)=x3+ax2 -4 x+5,若x=![]() 时,y=f(x)有极值.
时,y=f(x)有极值.
(1)求a的值;
(2)求y=f(x)在[-3,1]上的最大值.
【答案】(1)a=2;(2)13.
【解析】
(1)利用f′![]() =0,得到a的值;(2)确定y=f(x)在[﹣3,1]上的单调性,求出极值与端点的函数值,即可求最大值和最小值.
=0,得到a的值;(2)确定y=f(x)在[﹣3,1]上的单调性,求出极值与端点的函数值,即可求最大值和最小值.
(1)f′(x)=3x2+2ax-4,当x=![]() 时,y=f(x)有极值,则f′
时,y=f(x)有极值,则f′![]() =0,
=0,
可得4a-12+4=0.解得a=2.
(2)由(1)可得f(x)=x3+2x2-4x+5,∴f′(x)=3x2+4x-4,
令f′(x)=0,得x1=-2,x2=![]() .当x变化时,y、y′的取值及变化如下表:
.当x变化时,y、y′的取值及变化如下表:
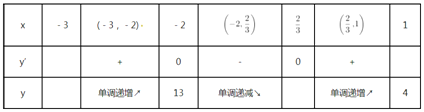
∴y=f(x)在[-3,1]上的最大值为13.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】某制造商![]() 月生产了一批乒乓球,随机抽样
月生产了一批乒乓球,随机抽样![]() 个进行检查,测得每个球的直径(单位:mm),将数据分组如下表
个进行检查,测得每个球的直径(单位:mm),将数据分组如下表
分组 | 频数 | 频率 |
| 10 | |
| 20 | |
| 50 | |
| 20 | |
合计 | 100 |

(1)请在上表中补充完成频率分布表(结果保留两位小数),并在上图中画出频率分布直方图;
(2)统计方法中,同一组数据常用该组区间的中点值(例如区间![]() 的中点值是
的中点值是![]() )作为代表.据此估计这批乒乓球直径的平均值(结果保留两位小数).
)作为代表.据此估计这批乒乓球直径的平均值(结果保留两位小数).
【题目】某大型企业人力资源部为了研究企业员工工作积极性和对待企业改革态度的关系,随机抽取了![]() 名员工进行问卷调查,其中
名员工进行问卷调查,其中![]() 的员工工作积极.经汇总调查,这
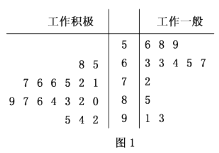
的员工工作积极.经汇总调查,这![]() 名员工是否支持企业改革的调查得分(百分制)如茎叶图(图
名员工是否支持企业改革的调查得分(百分制)如茎叶图(图![]() )所示.调查评价标准指出:调查得分不低于
)所示.调查评价标准指出:调查得分不低于![]() 分者为积极支持企业改革,调查得分低于70分者不太赞成企业改革.
分者为积极支持企业改革,调查得分低于70分者不太赞成企业改革.
(1)根据以上资料完成下面的![]() 列联表,结合数据能否有
列联表,结合数据能否有![]() 的把握认为员工的工作积极性与“是否积极支持企业改革”是有关的,并回答人力资源部的研究项目.
的把握认为员工的工作积极性与“是否积极支持企业改革”是有关的,并回答人力资源部的研究项目.
积极支持企业改革 | 不太赞成企业改革 | 总计 | |
工作积极 | |||
工作一般 | |||
总计 |
(2)现将![]() 名员工的调查得分分为如下
名员工的调查得分分为如下![]() 组:
组:![]() ,
,![]() ,
,![]() ,
,![]() ,
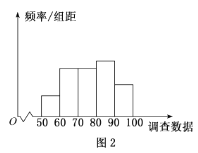
,![]() 其频率分布直方图如图
其频率分布直方图如图![]() 所示,这
所示,这![]() 名员工的调查数据得分的平均值可由茎叶图得到,记为
名员工的调查数据得分的平均值可由茎叶图得到,记为![]() ,由频率分布直方图得到的估计值记为
,由频率分布直方图得到的估计值记为![]() (同一组中的数据用该组区间的中点值作代表),
(同一组中的数据用该组区间的中点值作代表),![]() 与
与![]() 的误差值在
的误差值在![]() 以内,可以由
以内,可以由![]() 代替
代替![]() ,能否由
,能否由![]() 代替
代替![]() ?(提示:
?(提示:![]() 名员工的调查数据得分的和
名员工的调查数据得分的和![]() )
)
(3)该企业人力资源部从![]() 分以上的员工中任选
分以上的员工中任选![]() 名员工进行座谈,则所选员工的分数超过
名员工进行座谈,则所选员工的分数超过![]() 分的人数的数学期望是多少?
分的人数的数学期望是多少?
|
|
|
|
|
|
|
|
|
|
|
|
|
|
附: .
.