题目内容
【题目】已知圆C:(x﹣a)2+(y﹣2)2=4(a>0)及直线l:x﹣y+3=0.当直线l被圆C截得的弦长为![]() 时,求
时,求
(Ⅰ)a的值;
(Ⅱ)求过点(3,5)并与圆C相切的切线方程.
【答案】(Ⅰ)a=1;(Ⅱ)5x﹣12y+45=0或x=3.
【解析】
(Ⅰ)根据圆的方程找出圆心坐标与圆的半径,然后利用点到直线的距离公式表示出圆心到直线l的距离d,然后根据垂径定理得到弦心距,弦的一半及圆的半径成直角三角形,利用勾股对了列出关于a的方程,求出方程的解即可得到a的值,然后由a大于0,得到满足题意a的值;
(Ⅱ)把(Ⅰ)求出a的值代入圆的方程中确定出圆的方程,即可得到圆心的坐标,并判断得到已知点在圆外,分两种情况:当切线的斜率不存在时,得到x=3为圆的切线;当切线的斜率存在时,设切线的斜率为k,由(3,5)和设出的k写出切线的方程,根据直线与圆相切时圆心到直线的距离等于圆的半径,利用点到直线的距离公式表示出圆心到切线的距离d,让d等于圆的半径即可列出关于k的方程,求出方程的解即可得到k的值,把k的值代入所设的切线方程即可确定出切线的方程.综上,得到所有满足题意的切线的方程.
解:(Ⅰ)依题意可得圆心C(a,2),半径r=2,
则圆心到直线l:x﹣y+3=0的距离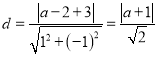 ,
,
由勾股定理可知![]() ,代入化简得|a+1|=2,
,代入化简得|a+1|=2,
解得a=1或a=﹣3,
又a>0,所以a=1;
(Ⅱ)由(1)知圆C:(x﹣1)2+(y﹣2)2=4,圆心坐标为(1,2),圆的半径r=2
由(3,5)到圆心的距离为![]() r=2,得到(3,5)在圆外,
r=2,得到(3,5)在圆外,
∴①当切线方程的斜率存在时,设方程为y﹣5=k(x﹣3)
由圆心到切线的距离d![]() r=2,
r=2,
化简得:12k=5,可解得![]() ,
,
∴切线方程为5x﹣12y+45=0;
②当过(3,5)斜率不存在直线方程为x=3与圆相切.
由①②可知切线方程为5x﹣12y+45=0或x=3.

 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案