题目内容
14.椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{2}}{2}$,C、D分别是椭圆的左右顶点,过椭圆右焦点F作弦AB(A,B,C,D不重合).当直线AB与x轴垂直,|AB|=$\sqrt{2}$.(Ⅰ)求椭圆的方程;
(Ⅱ)当△OAB的面积为$\frac{2}{3}$时,求直线AB的方程;
(Ⅲ)设直线AC、AD、BC、BD的斜率分别为k1,k2,k3,k4,证明:k1•k2•k3•k4为定值.
分析 (Ⅰ)由椭圆的离心率得得到a2=2b2,再由|AB|=$\frac{2{b}^{2}}{a}=\sqrt{2}$,联立求得a2=2,b2=1,则椭圆方程可求;
(Ⅱ)由△OAB的面积为$\frac{2}{3}$,可知弦AB的斜率一定存在,设直线AB的方程为y=k(x-1),联立直线方程和椭圆方程,利用弦长公式求得|AB|,再由点到直线的距离公式求得O到直线AB的距离d.代入三角形的面积公式求得k=±1.则直线AB的方程可求;
(Ⅲ)由题意求得C,D的坐标,再由斜率公式求得直线AC、AD、BC、BD的斜率,结合A,B在椭圆上整体运算求得k1•k2•k3•k4为定值.
解答 (Ⅰ)解:由题意知,$\frac{c}{a}=\frac{\sqrt{2}}{2}$,则$a=\sqrt{2}c$,b=c,a2=2b2,
把x=c代入椭圆方程得$y=\frac{{b}^{2}}{a}$,
∴|AB|=$\frac{2{b}^{2}}{a}=\sqrt{2}$,解得:a2=2,b2=1,
故椭圆方程为:$\frac{{x}^{2}}{2}+{y}^{2}=1$;
(Ⅱ)解:当直线AB的斜率不存在时,由题意可知,${S}_{△OAB}=\frac{1}{2}|AB|•d=\frac{1}{2}×\sqrt{2}×1=\frac{\sqrt{2}}{2}$,
故弦AB的斜率一定存在,且设直线AB的方程为y=k(x-1),
将直线的方程代入椭圆方程中,整理得到(1+2k2)x2-4k2x+2k2-2=0.
设A(x1,y1),B(x2,y2),
则${x}_{1}+{x}_{2}=\frac{4{k}^{2}}{1+2{k}^{2}},{x}_{1}{x}_{2}=\frac{2{k}^{2}-2}{1+2{k}^{2}}$,
|AB|=$\sqrt{1+{k}^{2}}|{x}_{1}-{x}_{2}|=\sqrt{1+{k}^{2}}•\frac{2\sqrt{2}\sqrt{1+{k}^{2}}}{1+2{k}^{2}}$=$\frac{2\sqrt{2}(1+{k}^{2})}{1+2{k}^{2}}$.
点O到直线AB的距离d=$\frac{|k|}{\sqrt{1+{k}^{2}}}$.
∴${S}_{△AOB}=\frac{1}{2}•|AB|•d=\frac{1}{2}•\frac{2\sqrt{2}(1+{k}^{2})}{1+2{k}^{2}}•\frac{|k|}{\sqrt{1+{k}^{2}}}$=$\frac{\sqrt{2}|k|(1+{k}^{2})}{1+2{k}^{2}}=\frac{2}{3}$.
整理得:k4+k2-2=0,解得:k=±1.
故直线AB的方程为x-y-1=0或x+y-1=0.
(Ⅲ)证明:由题意C($-\sqrt{2},0$),D($\sqrt{2},0$),
设A(x1,y1),B(x2,y2),
则${k}_{1}=\frac{{y}_{1}}{{x}_{1}+\sqrt{2}},{k}_{2}=\frac{{y}_{1}}{{x}_{1}-\sqrt{2}},{k}_{3}=\frac{{y}_{2}}{{x}_{2}+\sqrt{2}}$$,{k}_{4}=\frac{{y}_{2}}{{x}_{2}-\sqrt{2}}$.
∴${k}_{1}•{k}_{2}•{k}_{3}•{k}_{4}=\frac{{{y}_{1}}^{2}}{{{x}_{1}}^{2}-2}•\frac{{{y}_{2}}^{2}}{{{x}_{2}}^{2}-2}$,
又∵${{y}_{1}}^{2}=1-\frac{{{x}_{1}}^{2}}{2}$,${{y}_{2}}^{2}=1-\frac{{{x}_{2}}^{2}}{2}$,
∴k1•k2•k3•k4 =$\frac{-\frac{1}{2}({{x}_{1}}^{2}-2)}{{{x}_{1}}^{2}-2}•\frac{-\frac{1}{2}({{x}_{2}}^{2}-2)}{{{x}_{2}}^{2}-2}=\frac{1}{4}$.
点评 本题考查了椭圆方程的求法,考查了直线和椭圆的位置关系,体现了整体运算思想方法,是中高档题.

 习题精选系列答案
习题精选系列答案| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{3}-1}{2}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | $\sqrt{3}$一l |
| A. | 相交 | B. | 相切 | C. | 相离 | D. | 相交或相切 |

| A. | $\frac{1}{3}$ | B. | 1 | C. | $\frac{2}{3}$ | D. | $\frac{4}{3}$ |
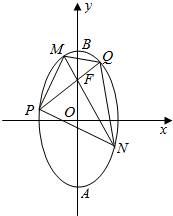 如图所示,椭圆长轴端点为点A、B、O为椭圆的中心,F为椭圆的上焦点,且$\overrightarrow{AF}•\overrightarrow{FB}=1,|\overrightarrow{OF}|=1$.
如图所示,椭圆长轴端点为点A、B、O为椭圆的中心,F为椭圆的上焦点,且$\overrightarrow{AF}•\overrightarrow{FB}=1,|\overrightarrow{OF}|=1$.