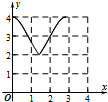题目内容
19．已知点P（m，n）在椭圆$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1上，则直线mx+ny+1=0与椭圆x2+y2=$\frac{1}{3}$的位置关系为（ ）| A． | 相交 | B． | 相切 | C． | 相离 | D． | 相交或相切 |
分析 由点P在椭圆上得到m，n的关系，把n用含有m的代数式表示，代入圆心到直线的距离中得到圆心到直线的距离小于等于圆的半径，则答案可求．
解答 解：∵P（m，n）在椭圆$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1上，
∴$\frac{{m}^{2}}{4}+\frac{{n}^{2}}{3}=1$，${n}^{2}=3-\frac{3}{4}{m}^{2}$，
圆x2+y2=$\frac{1}{3}$的圆心O（0，0）到直线mx+ny+1=0的距离：
d=$\frac{1}{\sqrt{{m}^{2}+{n}^{2}}}$=$\frac{1}{\sqrt{{m}^{2}+3-\frac{3}{4}{m}^{2}}}=\frac{1}{\sqrt{3+\frac{1}{4}{m}^{2}}}≤\frac{\sqrt{3}}{3}$，
∴直线mx+ny+1=0与椭圆x2+y2=$\frac{1}{3}$的位置关系为相交或相切．
故选：D．
点评 本题考查了椭圆的简单性质，考查了直线和圆的位置关系，是基础题．
练习册系列答案
名校课堂系列答案
相关题目
9．M、N分别是椭圆$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1（a＞b＞0）的左、右顶点，椭圆上异于M、N于点P满足kPM•kPN=-$\frac{1}{4}$，则椭圆的离心率为（ ）
| A． | $\frac{{\sqrt{2}}}{2}$ | B． | $\frac{{\sqrt{3}}}{3}$ | C． | $\frac{{\sqrt{3}}}{2}$ | D． | $\frac{1}{3}$ |
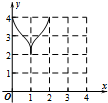
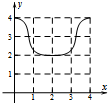
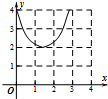
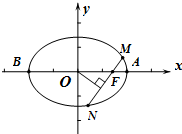如图：已知方程为$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{2}$=1的椭圆，A，B为顶点，过右焦点的弦MN的长度为y，中心O到弦MN的距离为d，点M从右顶点A开始按逆时针方向在椭圆上移动到B停止，当0°≤∠MFA≤90°时，记x=d，当90°＜∠MFA≤180°，记x=2$\sqrt{2}$-d，函数y=f（x）图象是（ ）
4．椭圆x2+$\frac{y^2}{4}$=1的离心率为（ ）
| A． | $\frac{{\sqrt{5}}}{2}$ | B． | $\frac{{\sqrt{3}}}{2}$ | C． | $\sqrt{5}$ | D． | $\sqrt{3}$ |
8．函数f（x）=$\frac{{x}^{2}（x+1）}{x+1}$是（ ）
| A． | 奇函数 | B． | 偶函数 | ||
| C． | 既是奇函数又是偶函数 | D． | 非奇非偶函数 |