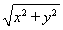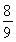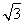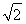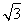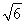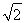Question

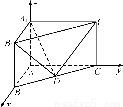
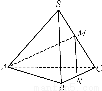
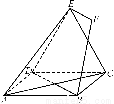
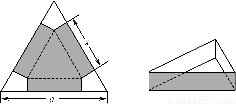
在边长为a的正三角形铁皮的三个角切去三个全等的四边形，再把它的边沿虚线折起(如图)，做成一个无盖的正三角形底铁皮箱，当箱底边长为多少时，箱子容积最大？最大容积是多少？

 

 

Answer 1

当箱子底边长为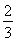a时，箱子容积最大，最大值为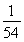a3.

【解析】设箱底边长为x，则箱高为h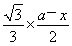＝(0<x<a)，

箱子的容积为V(x)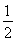＝x2×sin60°×h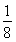＝ax2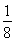－x3(0<x<a)．

由V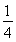′(x)＝ax－x2＝0，解得x1＝0(舍)，x2＝a，

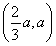且当x∈时，V′(x)>0；当x∈时，V′(x)<0，

所以函数V(x)在x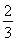＝a处取得极大值，

这个极大值就是函数V(x)的最大值：V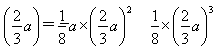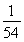＝a3.

答：当箱子底边长为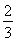a时，箱子容积最大，最大值为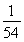a3.