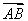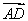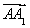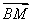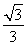题目内容
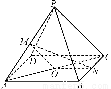
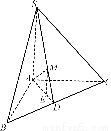
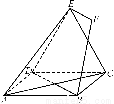
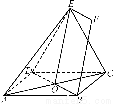
如图，正方形ABCD和三角形ACE所在的平面互相垂直．EF∥BD，AB＝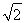
EF.求证：
(1)BF∥平面ACE；
(2)BF⊥BD.
（1）见解析（2）见解析
【解析】(1)AC与BD交于O点，连结EO.
正方形ABCD中，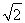
BO＝AB，又因为AB＝
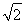EF，
∴BO＝EF，又因为EF∥BD，∴EFBO是平行四边形
∴BF∥EO，又∵BF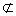
平面ACE，EO
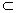平面ACE，
∴BF∥平面ACE.
(2)正方形ABCD中，AC⊥BD，又因为正方形ABCD和三角形ACE所在的平面互相垂直，
BD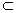
平面ABCD，平面ABCD∩平面ACE＝AC，∴BD⊥平面ACE，∵EO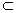平面ACE
∴BD⊥EO，∵EO∥BF，∴BF⊥BD.
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
