题目内容
【题目】已知椭圆 ![]() +
+ ![]() =1(a>b>0)右顶点与右焦点的距离为
=1(a>b>0)右顶点与右焦点的距离为 ![]() ﹣1,短轴长为2
﹣1,短轴长为2 ![]() . (Ⅰ)求椭圆的方程;
. (Ⅰ)求椭圆的方程;
(Ⅱ)过左焦点F的直线与椭圆分别交于A、B两点,若三角形OAB的面积为 ![]() ,求直线AB的方程.
,求直线AB的方程.
【答案】解:(Ⅰ)由题意, 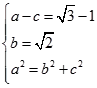 ,解得a=
,解得a= ![]() ,c=1. 即椭圆方程为
,c=1. 即椭圆方程为 ![]() =1
=1
(Ⅱ)当直线AB与x轴垂直时,|AB|= ![]() ,此时S=
,此时S= ![]() 不符合题意,故舍掉;
不符合题意,故舍掉;
当直线AB与x轴不垂直时,设直线 AB的方程为:y=k(x+1),代入消去y得:(2+3k2)x2+6k2x+(3k2﹣6)=0.
设A(x1 , y1),B(x2 , y2),则 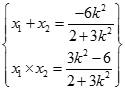 ,所以|AB|=
,所以|AB|= ![]() .
.
原点到直线的AB距离d= ![]() ,
,
所以三角形的面积S= 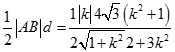 .
.
由S= ![]() 可得k2=2,∴k=±
可得k2=2,∴k=± ![]() ,
,
所以直线AB: ![]() =0或AB:
=0或AB: ![]() =0
=0
【解析】(Ⅰ)根据椭圆右顶点与右焦点的距离为 ![]() ,短轴长为
,短轴长为 ![]() ,可得
,可得 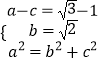 ,由此,即可求得椭圆方程;(Ⅱ)当直线AB与x轴垂直时,
,由此,即可求得椭圆方程;(Ⅱ)当直线AB与x轴垂直时, ![]() ,此时
,此时 ![]() 不符合题意;当直线AB与x轴不垂直时,设直线 AB的方程为:y=k(x+1),代入消去y得,进而可求三角形的面积,利用
不符合题意;当直线AB与x轴不垂直时,设直线 AB的方程为:y=k(x+1),代入消去y得,进而可求三角形的面积,利用 ![]() ,即可求出直线AB的方程.
,即可求出直线AB的方程.
【考点精析】认真审题,首先需要了解椭圆的标准方程(椭圆标准方程焦点在x轴:![]() ,焦点在y轴:
,焦点在y轴:![]() ).
).

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目