题目内容
【题目】已知定圆C：x2+（y﹣3）2=4，定直线m；x+3y+6=0，过A（﹣1，0）的一条动直线l与直线相交于N，与圆C相交于P，Q两点，
（1）当l与m垂直时，求出N点的坐标，并证明：l过圆心C；
（2）当|PQ|=2 
时，求直线l的方程．
【答案】
（1）解：因为l与m垂直，直线m：x+3y+6=0的斜率为﹣ 
，
所以直线l的斜率为3，
所以l的方程为y﹣0=3（x+1），即3x﹣y+3=0．
联立 
，解得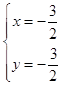 
，
即有N（﹣ 
，﹣ ），
代入圆心（0，3），有0﹣3+3=0成立，
所以直线l过圆心C（0，3）
（2）解：由|PQ|=2 
得，圆心C到直线l的距离d=1，
设直线l的方程为x﹣ny+1=0，则由d= 
=1．
解得n=0，或n= 
，
所以直线l的方程为x+1=0或4x﹣3y+4=0
【解析】（1）运用两直线垂直的条件：斜率之积为﹣1，求得l的斜率，可得直线l的方程，联立直线m的方程，可得交点N，代入圆心，可得直线l过圆心；（2）由|PQ|=2 得，圆心C到直线l的距离d=1，设直线l的方程为x﹣ny+1=0，求得n的值，可得直线l的方程．
练习册系列答案
相关题目
