题目内容
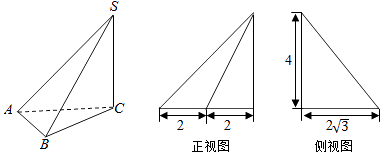
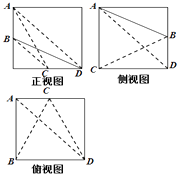
【题目】如图,在四面体A﹣BCD中,AD⊥平面BCD,BC⊥CD,AD=2,BD=2 ![]() .M是AD的中点,P是BM的中点,点Q在线段AC上,且AQ=3QC.
.M是AD的中点,P是BM的中点,点Q在线段AC上,且AQ=3QC. 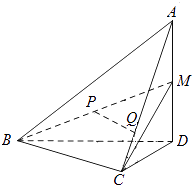
(1)证明:PQ∥平面BCD;
(2)若二面角C﹣BM﹣D的大小为60°,求∠BDC的大小.
【答案】
(1)解:取BD的中点O,在线段CD上取点F,使得DF=3CF,连接OP、OF、FQ
∵△ACD中,AQ=3QC且DF=3CF,∴QF∥AD且QF= ![]() AD
AD
∵△BDM中,O、P分别为BD、BM的中点
∴OP∥DM,且OP= ![]() DM,结合M为AD中点得:OP∥AD且OP=
DM,结合M为AD中点得:OP∥AD且OP= ![]() AD
AD
∴OP∥QF且OP=QF,可得四边形OPQF是平行四边形
∴PQ∥OF
∵PQ平面BCD且OF平面BCD,∴PQ∥平面BCD
(2)解:过点C作CG⊥BD,垂足为G,过G作GH⊥BM于H,连接CH
∵AD⊥平面BCD,CG平面BCD,∴AD⊥CG
又∵CG⊥BD,AD、BD是平面ABD内的相交直线
∴CG⊥平面ABD,结合BM平面ABD,得CG⊥BM
∵GH⊥BM,CG、GH是平面CGH内的相交直线
∴BM⊥平面CGH,可得BM⊥CH
因此,∠CHG是二面角C﹣BM﹣D的平面角,可得∠CHG=60°
设∠BDC=θ,可得
Rt△BCD中,CD=BDcosθ=2 ![]() cosθ,CG=CDsinθ=2
cosθ,CG=CDsinθ=2 ![]() sinθcosθ,BG=BCsinθ=2
sinθcosθ,BG=BCsinθ=2 ![]() sin2θ
sin2θ
Rt△BMD中,HG= ![]() =
= ![]() ;Rt△CHG中,tan∠CHG=
;Rt△CHG中,tan∠CHG= ![]() =
= ![]()
∴tanθ= ![]() ,可得θ=60°,即∠BDC=60°
,可得θ=60°,即∠BDC=60°
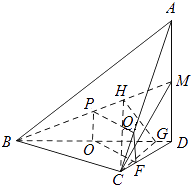
【解析】(1)取BD的中点O,在线段CD上取点F,使得DF=3CF,连接OP、OF、FQ.根据平行线分线段成比例定理结合三角形的中位线定理证出四边形OPQF是平行四边形,从而PQ∥OF,再由线面平行判定定理,证出PQ∥平面BCD;(2)过点C作CG⊥BD,垂足为G,过G作GH⊥BM于H,连接CH.根据线面垂直的判定与性质证出BM⊥CH,因此∠CHG是二面角C﹣BM﹣D的平面角,可得∠CHG=60°.设∠BDC=θ,用解直角三角形的方法算出HG和CG关于θ的表达式,最后在Rt△CHG中,根据正切的定义得出tan∠CHG= ![]() =
= ![]() ,从而得到tanθ=
,从而得到tanθ= ![]() ,由此可得∠BDC.
,由此可得∠BDC.

 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案