题目内容
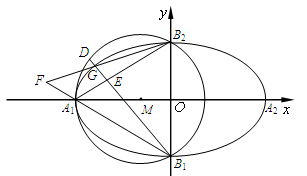
如图,已知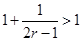 ,
, ,
,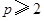 ,
, 分别是椭圆
分别是椭圆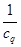 的四个顶点,△
的四个顶点,△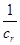 是一个边长为2的等边三角形,其外接圆为圆
是一个边长为2的等边三角形,其外接圆为圆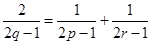 .
.
(1)求椭圆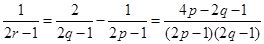 及圆
及圆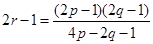 的方程;
的方程;
(2)若点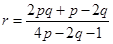 是圆
是圆 劣弧
劣弧 上一动点(点
上一动点(点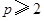 异于端点
异于端点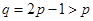 ,
,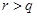 ),直线
),直线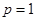 分别交线段
分别交线段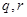 ,椭圆
,椭圆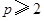 于点
于点 ,
, ,直线
,直线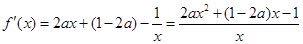 与
与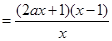 交于点
交于点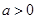 .
.
(ⅰ)求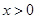 的最大值;
的最大值;
(ⅱ)试问:.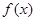 .,
., 两点的横坐标之和是否为定值?若是,求出该定值;若不是,说明理由.
两点的横坐标之和是否为定值?若是,求出该定值;若不是,说明理由.
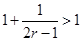 ,
, ,
,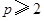 ,
, 分别是椭圆
分别是椭圆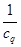 的四个顶点,△
的四个顶点,△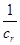 是一个边长为2的等边三角形,其外接圆为圆
是一个边长为2的等边三角形,其外接圆为圆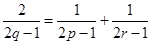 .
.(1)求椭圆
 及圆
及圆 的方程;
的方程;(2)若点
 是圆
是圆 劣弧
劣弧 上一动点(点
上一动点(点 异于端点
异于端点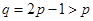 ,
,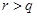 ),直线
),直线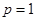 分别交线段
分别交线段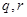 ,椭圆
,椭圆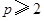 于点
于点 ,
, ,直线
,直线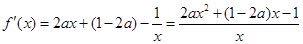 与
与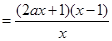 交于点
交于点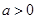 .
.(ⅰ)求
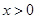 的最大值;
的最大值;(ⅱ)试问:.
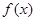 .,
.,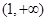 两点的横坐标之和是否为定值?若是,求出该定值;若不是,说明理由.
两点的横坐标之和是否为定值?若是,求出该定值;若不是,说明理由.
(1)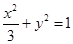 ,
, ,(2)(ⅰ)
,(2)(ⅰ) ,(ⅱ)
,(ⅱ) .
.
 ,
, ,(2)(ⅰ)
,(2)(ⅰ) ,(ⅱ)
,(ⅱ)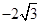 .
.试题分析:(1)求椭圆标准方程,只需两个独立条件. 由题意知,
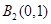 ,
,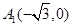 ,所以
,所以 ,
,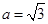 ,所以椭圆
,所以椭圆 的方程为
的方程为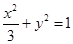 ,求圆的方程,有两个选择,一是求圆的标准方程,确定圆心与半径,二是求圆的一般方程,只需代入圆上三个点的坐标.本题两个方法皆简单,如易得圆心
,求圆的方程,有两个选择,一是求圆的标准方程,确定圆心与半径,二是求圆的一般方程,只需代入圆上三个点的坐标.本题两个方法皆简单,如易得圆心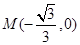 ,
, ,所以圆
,所以圆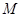 的方程为
的方程为
(2)(ⅰ)本题关键分析出比值
 暗示的解题方向,由于点
暗示的解题方向,由于点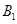 在
在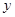 轴上,所以
轴上,所以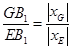 ,因此解题方向为利用斜率分别表示出点
,因此解题方向为利用斜率分别表示出点 与点
与点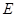 的横坐标. 设直线
的横坐标. 设直线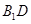 的方程为
的方程为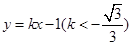 ,与直线
,与直线 的方程
的方程 联立,解得点
联立,解得点 ,联立
,联立 ,消去
,消去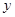 并整理得,
并整理得, ,解得点
,解得点 ,因此
,因此
 当且仅当
当且仅当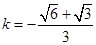 时,取“=”,所以
时,取“=”,所以 的最大值为
的最大值为 .(ⅱ)求出点
.(ⅱ)求出点 的横坐标,分析与点
的横坐标,分析与点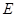 的横坐标的和是否为常数. 直线.
的横坐标的和是否为常数. 直线. .的方程为
.的方程为 ,与直线
,与直线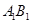 的方程
的方程 联立,解得点
联立,解得点 ,所以
,所以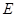 、
、 两点的横坐标之和为
两点的横坐标之和为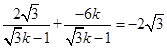 .
.试题解析:(1)由题意知,
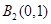 ,
,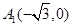 ,
,所以
 ,
,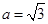 ,所以椭圆
,所以椭圆 的方程为
的方程为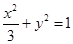 , 2分
, 2分易得圆心
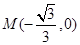 ,
, ,所以圆
,所以圆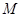 的方程为
的方程为 . 4分
. 4分(2)解:设直线
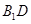 的方程为
的方程为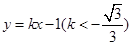 ,
,与直线
 的方程
的方程 联立,解得点
联立,解得点 , 6分
, 6分联立
 ,消去
,消去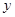 并整理得,
并整理得, ,解得点
,解得点 ,
,9分
(ⅰ)
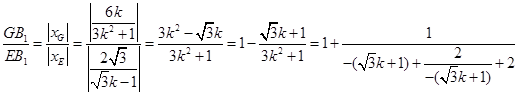
 ,当且仅当
,当且仅当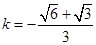 时,取“=”,
时,取“=”,所以
 的最大值为
的最大值为 . 12分
. 12分(ⅱ)直线
 的方程为
的方程为 ,
,与直线
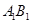 的方程
的方程 联立,解得点
联立,解得点 , 14分
, 14分所以
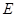 、
、 两点的横坐标之和为
两点的横坐标之和为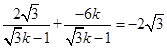 .
.故
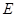 、
、 两点的横坐标之和为定值,该定值为
两点的横坐标之和为定值,该定值为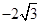 . 16分
. 16分
练习册系列答案
 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案
相关题目
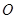 的抛物线
的抛物线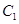 的焦点
的焦点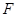 与椭圆
与椭圆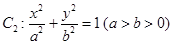 的右焦点重合,
的右焦点重合,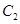 在第一和第四象限的交点分别为
在第一和第四象限的交点分别为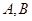 .
.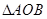 是边长为
是边长为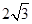 的正三角形,求抛物线
的正三角形,求抛物线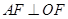 ,求椭圆
,求椭圆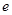 .
.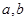 ,定义
,定义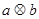 的算法原理如右侧程序框图所示.设
的算法原理如右侧程序框图所示.设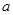 为函数
为函数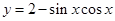 的最大值,
的最大值,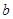 为双曲线
为双曲线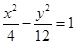 的离心率,则计算机执行该运算后输出的结果是( )
的离心率,则计算机执行该运算后输出的结果是( )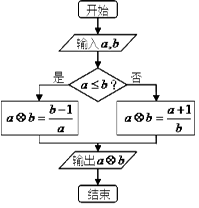
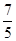
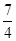
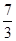
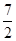
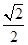 .
.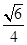 .若A、B两点关于x轴对称,E为线段AB的中点,射线OE交椭圆C于点P.如果
.若A、B两点关于x轴对称,E为线段AB的中点,射线OE交椭圆C于点P.如果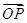 =t
=t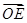 ,求实数t的值.
,求实数t的值.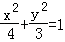 的左、右顶点分别为A1、A2,点P在C上且直线PA2斜率的取值范围是[﹣2,﹣1],那么直线PA1斜率的取值范围是( )
的左、右顶点分别为A1、A2,点P在C上且直线PA2斜率的取值范围是[﹣2,﹣1],那么直线PA1斜率的取值范围是( )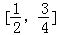
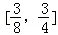
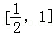
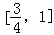
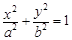 的一个焦点为
的一个焦点为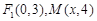
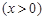 为椭圆C上一点,△MOF2的面积为
为椭圆C上一点,△MOF2的面积为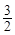 .
.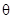 是任意实数,则方程
是任意实数,则方程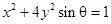 所表示的曲线一定不是( )
所表示的曲线一定不是( )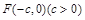 是双曲线
是双曲线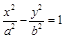 的左焦点,离心率为e,过F且平行于双曲线渐近线的直线与圆
的左焦点,离心率为e,过F且平行于双曲线渐近线的直线与圆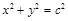 交于点P,且点P在抛物线
交于点P,且点P在抛物线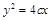 上,则e2 =( )
上,则e2 =( )