题目内容
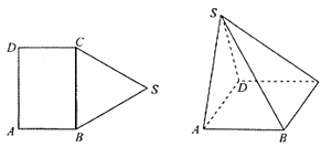
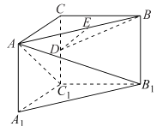
【题目】如图,在三棱锥![]() 中,
中,![]() 、
、![]() 、
、![]() 分别为棱
分别为棱![]() 、
、![]() 、
、![]() 的中点,
的中点,![]() 平面
平面![]() ,
,![]() ,
,![]() ,
,![]() ,则( )
,则( )
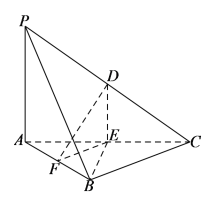
A.三棱锥![]() 的体积为
的体积为![]()
B.直线![]() 与直线
与直线![]() 垂直
垂直
C.平面![]() 截三棱锥
截三棱锥![]() 所得的截面面积为
所得的截面面积为![]()
D.点![]() 与点
与点![]() 到平面
到平面![]() 的距离相等
的距离相等
【答案】ACD
【解析】
根据锥体的体积公式可判断A选项的正误;假设![]() ,推导出
,推导出![]() 平面
平面![]() ,结合题意可判断B选项的正误;取
,结合题意可判断B选项的正误;取![]() 的中点
的中点![]() ,计算出四边形
,计算出四边形![]() 的面积,可判断C选项的正误;证明出
的面积,可判断C选项的正误;证明出![]() 平面
平面![]() ,可判断D选项的正误.
,可判断D选项的正误.
对于A选项,![]() 、
、![]() 分别为
分别为![]() 、
、![]() 的中点,则
的中点,则![]() ,且
,且![]() ,
,
![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
![]() 为
为![]() 的中点,
的中点,![]() ,
,![]() ,
,
所以,![]() ,A选项正确;
,A选项正确;
对于B选项,![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,![]() ,
,
又![]() ,即
,即![]() ,
,![]() ,
,![]() 平面
平面![]() ,
,
![]() 、
、![]() 分别为
分别为![]() 、
、![]() 的中点,
的中点,![]() ,
,![]() 平面
平面![]() ,
,
![]() 平面
平面![]() ,
,![]() ,
,
![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,![]() ,
,
![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,![]() ,
,
假设![]() ,
,![]() ,
,![]() 平面
平面![]() ,
,
而过点![]() 有且只有一条直线与平面
有且只有一条直线与平面![]() 垂直,故B选项错误;
垂直,故B选项错误;
对于C选项,取![]() 的中点
的中点![]() ,连接
,连接![]() 、
、![]() ,
,

![]() 、
、![]() 分别为
分别为![]() 、
、![]() 的中点,
的中点,![]() 且
且![]() ,
,
同理可得![]() 且
且![]() ,
,![]() 且
且![]() ,
,
所以,四边形![]() 为平行四边形,则平面
为平行四边形,则平面![]() 截三棱锥
截三棱锥![]() 所得的截面为平行四边形
所得的截面为平行四边形![]() ,
,
易知![]() ,且
,且![]() ,
,![]() ,所以,
,所以,![]() ,
,
故C选项正确;
对于D选项,![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
所以,点![]() 与点
与点![]() 到平面
到平面![]() 的距离相等,故D选项正确.
的距离相等,故D选项正确.
故选:ACD.

 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案【题目】某社区消费者协会为了解本社区居民网购消费情况,随机抽取了100位居民作为样本,就最近一年来网购消费金额(单位:千元),网购次数和支付方式等进行了问卷调査.经统计这100位居民的网购消费金额均在区间![]() 内,按
内,按![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 分成6组,其频率分布直方图如图所示.
分成6组,其频率分布直方图如图所示.
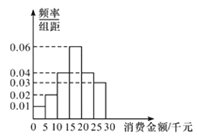
(1)估计该社区居民最近一年来网购消费金额的中位数;
(2)将网购消费金额在20千元以上者称为“网购迷”,补全下面的![]() 列联表,并判断有多大把握认为“网购迷与性别有关系”;
列联表,并判断有多大把握认为“网购迷与性别有关系”;
男 | 女 | 合计 | |
网购迷 | 20 | ||
非网购迷 | 45 | ||
合计 | 100 |
(3)调査显示,甲、乙两人每次网购采用的支付方式相互独立,两人网购时间与次数也互不. 影响.统计最近一年来两人网购的总次数与支付方式,所得数据如下表所示:
网购总次数 | 支付宝支付次数 | 银行卡支付次数 | 微信支付次数 | |
80 | 40 | 16 | 24 | |
乙 | 90 | 60 | 18 | 12 |
将频率视为概率,若甲、乙两人在下周内各自网购2次,记两人采用支付宝支付的次数之和为![]() ,求
,求![]() 的数学期望.
的数学期望.
附:观测值公式: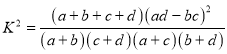
临界值表:
| 0.01 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |