题目内容
【题目】一年之计在于春,一日之计在于晨,春天是播种的季节,是希望的开端.某种植户对一块地的![]() 个坑进行播种,每个坑播3粒种子,每粒种子发芽的概率均为
个坑进行播种,每个坑播3粒种子,每粒种子发芽的概率均为![]() ,且每粒种子是否发芽相互独立.对每一个坑而言,如果至少有两粒种子发芽,则不需要进行补播种,否则要补播种.
,且每粒种子是否发芽相互独立.对每一个坑而言,如果至少有两粒种子发芽,则不需要进行补播种,否则要补播种.
(1)当![]() 取何值时,有3个坑要补播种的概率最大?最大概率为多少?
取何值时,有3个坑要补播种的概率最大?最大概率为多少?
(2)当![]() 时,用
时,用![]() 表示要补播种的坑的个数,求
表示要补播种的坑的个数,求![]() 的分布列与数学期望.
的分布列与数学期望.
【答案】(1)当![]() 或
或![]() 时,有3个坑要补播种的概率最大,最大概率为
时,有3个坑要补播种的概率最大,最大概率为![]() ; (2)见解析.
; (2)见解析.
【解析】
(1)将有3个坑需要补种表示成n的函数,考查函数随n的变化情况,即可得到n为何值时有3个坑要补播种的概率最大.(2)n=4时,X的所有可能的取值为0,1,2,3,4.分别计算出每个变量对应的概率,列出分布列,求期望即可.
(1)对一个坑而言,要补播种的概率![]() ,
,
有3个坑要补播种的概率为![]() .
.
欲使![]() 最大,只需
最大,只需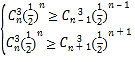 ,
,
解得![]() ,因为
,因为![]() ,所以
,所以![]()
当![]() 时,
时,![]() ;
;
当![]() 时,
时,![]() ;
;
所以当![]() 或
或![]() 时,有3个坑要补播种的概率最大,最大概率为
时,有3个坑要补播种的概率最大,最大概率为![]() .
.
(2)由已知,![]() 的可能取值为0,1,2,3,4.
的可能取值为0,1,2,3,4.![]() ,
,
所以![]() 的分布列为
的分布列为
| 0 | 1 | 2 | 3 | 4 |
|
|
|
|
|
|
![]() 的数学期望
的数学期望![]() .
.

练习册系列答案
相关题目