题目内容
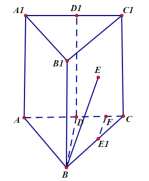
【题目】如图,正三棱柱![]() 中,
中,![]() 、点
、点![]() 为
为![]() 中点,点
中点,点![]() 为四边形
为四边形![]() 内(包含边界)的动点则以下结论正确的是( )
内(包含边界)的动点则以下结论正确的是( )

A.![]()
B.若![]() 平面
平面![]() ,则动点
,则动点![]() 的轨迹的长度等于
的轨迹的长度等于![]()
![]()
C.异面直线![]() 与
与![]() ,所成角的余弦值为
,所成角的余弦值为![]()
D.若点![]() 到平面
到平面![]() 的距离等于
的距离等于![]() ,则动点
,则动点![]() 的轨迹为抛物线的一部分
的轨迹为抛物线的一部分
【答案】BCD
【解析】
根据空间向量的加减法运算以及通过建立空间直角坐标系求解,逐项判断,进而可得到本题答案.
解析:对于选项A,![]() ,选项A错误;
,选项A错误;
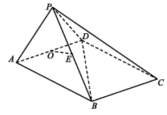
对于选项B,过点![]() 作
作![]() 的平行线交
的平行线交![]() 于点
于点![]() .
.
以![]() 为坐标原点,
为坐标原点,![]() 分别为
分别为![]() 轴的正方向建立空间直角坐标系
轴的正方向建立空间直角坐标系![]() .
.
设棱柱底面边长为![]() ,侧棱长为
,侧棱长为![]() ,则
,则![]() ,
,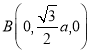 ,
,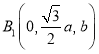 ,
,![]() ,所以
,所以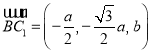 ,
,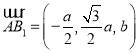 .
.
∵![]() ,∴
,∴![]() ,
,
即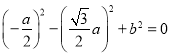 ,解得
,解得![]() .
.
因为![]() 平面
平面![]() ,则动点
,则动点![]() 的轨迹的长度等于
的轨迹的长度等于![]() .选项B正确.
.选项B正确.
对于选项C,在选项A的基础上,![]() ,
,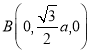 ,
,![]() ,
,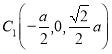 ,所以
,所以![]() ,
,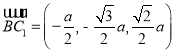 ,
,
因为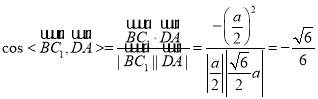 ,所以异面直线
,所以异面直线![]() 所成角的余弦值为
所成角的余弦值为![]() ,选项C正确.
,选项C正确.
对于选项D,设点E在底面ABC的射影为![]() ,作
,作![]() 垂直于
垂直于![]() ,垂足为F,若点E到平面
,垂足为F,若点E到平面![]() 的距离等于
的距离等于![]() ,即有
,即有![]() ,又因为在
,又因为在![]() 中,
中,![]() ,得
,得![]() ,其中
,其中![]() 等于点E到直线
等于点E到直线![]() 的距离,故点E满足抛物线的定义,另外点E为四边形
的距离,故点E满足抛物线的定义,另外点E为四边形![]() 内(包含边界)的动点,所以动点E的轨迹为抛物线的一部分,故D正确.
内(包含边界)的动点,所以动点E的轨迹为抛物线的一部分,故D正确.
故选:BCD

练习册系列答案
相关题目